Термодинамические параметры

Тепловые машины. Формула КПД в термодинамике

Тепловая машина, в простейшем случае, состоит из нагревателя, холодильника и рабочего тела. Нагреватель сообщает тепло рабочему телу, оно совершает работу, затем охлаждается холодильником, и все повторяется вновь. Типичным примером тепловой машины является двигатель внутреннего сгорания.

Коэффициент полезного действия тепловой машины вычисляется по формуле

Вот мы и собрали основные формулы термодинамики, которые пригодятся в решении задач. Конечно, это не все все формулы из темы термодинамика, но их знание действительно может сослужить хорошую службу. А если возникнут вопросы  – помните о студенческом сервисе, специалисты которого готовы в любой момент прийти на выручку.

Причина возникновения давления в газах

Давление газа нельзя объяснить теми же причинами, что и давление твердого тела на опору. Расстояние, на которое удалены молекулы газообразной среды, существенно больше. В результате хаотичного движения они сталкиваются между собой и со стенками сосуда, который они занимают. Давление газа на стенки сосуда и вызвано ударами его молекул.

Данный параметр увеличивается по мере того, как нарастает сила ударов молекул о стенки. Газ характеризуется одинаковым давлением во всех направлениях, которое является следствием хаотичного движения огромного числа молекул.

Примечание

Важно отметить, что газ оказывает давление на дно и стенки сосуда, объем которого он занимает, во всех направления равномерно. В связи с этим, воздушный шарик сохраняет форму, несмотря на то, что его оболочка достаточно эластична

Перед тем как транспортировать или отправить на хранение газообразные вещества, их сильно сжимают. В этом случае давление газа увеличивается. Его помещают в специальные баллоны из стали высокой прочности. Такие емкости необходимы для хранения сжатого воздуха на подводных лодках и кислорода, предназначенного для сварки металлов.

Свойства давления газа:

1. Если объем уменьшается, то давление газа возрастает, а во время увеличения объема, давление будет снижаться при постоянных величинах массы и температуры вещества.
2. Газ, находящийся в закрытом сосуде, характеризуется давлением, которое возрастает по мере увеличения температуры вещества при условии постоянства его массы и объема.
3. В том случае, когда масса газа увеличивается, его давление также будет возрастать и наоборот.

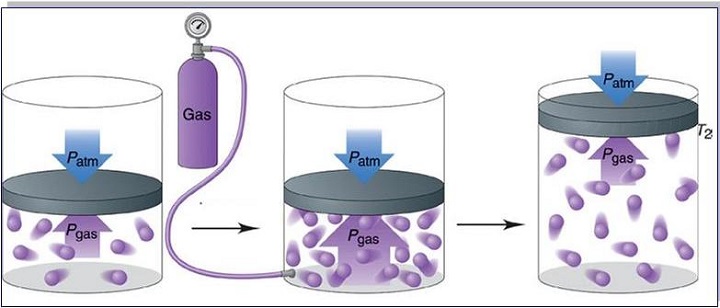
Запись формул для определения давления газа начинают с выяснения причин, по которым оно возникает в рассматриваемой системе. Исходя из физического смысла, давление представляет собой величину, равную отношению силы, перпендикулярно воздействующей на некоторое основание, к площади этого основания:

\(P=\frac{F}{S}\)

Как было отмечено ранее, для идеальной газовой системы характерен лишь один тип взаимодействия — это абсолютно упругие столкновения. В процессе частицы передают количество движения Δp стенкам сосуда в течение времени соударения Δt. В данном случае применим второй закон Ньютона:

\(F*Δt = Δp\)

Таким образом, конкретно сила F является причиной формирования давления на стенки сосуда. Данная величина F, производимая одной частицей, незначительна. Однако, когда количество частиц огромно, они в совокупности создают ощутимый эффект, проявляемый в виде наличия давления в сосуде.

Уравнение состояния идеального газа

Состояние идеального газа характеризуют три параметра: давление, объём и температура. Зависимость между ними описывается уравнением:

где р — давление,

V_M — молярный объём,

R — универсальная газовая постоянная,

T — абсолютная температура (градусы Кельвина).

Так как V_M = Vn, где V — объём, n — количество вещества, а n = m/M, то

где m — масса газа, М — молярная масса. Это уравнение называется уравнением Менделеева-Клайперона.

При постоянной массе уравнение приобретает вид:

Это уравнение называют объединённым газовым законом.

Используя закон Менделеева-Клайперона, можно определить один из параметров газа, если известны два других.

Уравнение состояния для смеси газов

Уравнение состояния идеального газа описывает макроскопические параметры конкретного газа. Однако, в задачах нередко необходимо определять параметры смеси газов с разными молярными массами.

В этом случае применяется закон Дальтона.

Рис. 3. Закон Дальтона.

Давление для каждой из компонент газа вычисляется отдельно, как если бы эта компонента была бы одна. Такое давление называется парциальным, а потом, общее давление смеси, в соответствии с законом Дальтона находится, как сумма парциальных давлений всех компонент.

Что мы узнали?

Уравнение состояния идеального газа связывает объем, давление и температуру (макроскопические газовые параметры) с общей и молярной массой газа. Данное уравнение называется уравнением Менделеева-Клапейрона. Для расчета параметров смеси газов используется закон Дальтона.

1. /10

   Вопрос 1 из 10

   Уравнение состояния идеального газа выводится на основе …

   • закона всемирного тяготения Ньютона
   • электродинамики Максвелла
   • молекулярно-кинетической теории
   • теории относительности Эйнштейна

Уравнение Менделеева-Клапейрона

Уравнение Клапейрона хорошо описывает изменение в газовых процессах макроскопических параметров некоторого количества газа. Однако, заранее сказать, какими будут эти параметры для конкретной массы некоторого конкретного газа, нельзя. Константа, присутствующая в уравнении Клапейрона должна вычисляться каждый раз заново.

В 1874 г Д. Менделеев сделал вывод, что эта константа прямо пропорциональная количеству вещества газа, то есть отношению общей массы газа $m$ к его молярной массе $М$:

$${pV\over T} \thicksim \nu= {m\over M}$$

Рис. 2. Д. Менделеев.

А поскольку один моль любого газа в одинаковых условиях занимает один и тот же объем, можно ввести специальный коэффициент, $R=8.31 {Дж \over моль × К}$. С этим коэффициентом уравнение состояния идеального газа получит вид:

$${pV\over T} ={m\over M}R$$

Значение температуры чаще всего переносят в правую часть формулы. Окончательно имеем:

$$pV ={m\over M}RT$$

Уравнение состояния идеального газа в таком виде называется уравнением Менделеева-Клапейрона. Данное уравнение связывает макроскопические параметры газа с его физическими параметрами.

Постоянная R, присутствующая в уравнении, называется универсальной газовой постоянной. Она равна произведению числа Авогадро на постоянную Больцмана, и представляет количество тепла, которое необходимо сообщить одному молю газа для увеличения его температуры на один кельвин.

Идеальный газ

Идеальный газ – это идеализация, как и материальная точка. Молекулы такого газа являются материальными точками, а соударения молекул – абсолютно упругие. Взаимодействием же молекул на расстоянии пренебрегаем. В задачах по термодинамике реальные газы часто принимаются за идеальные. Так гораздо легче жить, и не нужно иметь дела с массой новых членов в уравнениях.

Итак, что происходит с молекулами идеального газа? Да, они движутся! И резонно спросить, с какой скоростью? Конечно, помимо скорости молекул нас интересует еще и общее состояние нашего газа. Какое давление P он оказывает на стенки сосуда, какой объем V занимает, какая у него температура T.

Для того, чтобы узнать все это, есть уравнение состояния идеального газа, или уравнение Клапейрона-Менделеева

Здесь m – масса газа, M – его молекулярная масса (находим по таблице Менделеева), R – универсальная газовая постоянная, равная 8,3144598(48) Дж/(моль*кг).

Универсальная газовая постоянная может быть выражена через другие константы (постоянная Больцмана и число Авогадро)

Массу, в свою очередь, можно вычислить, как произведение плотности и объема.

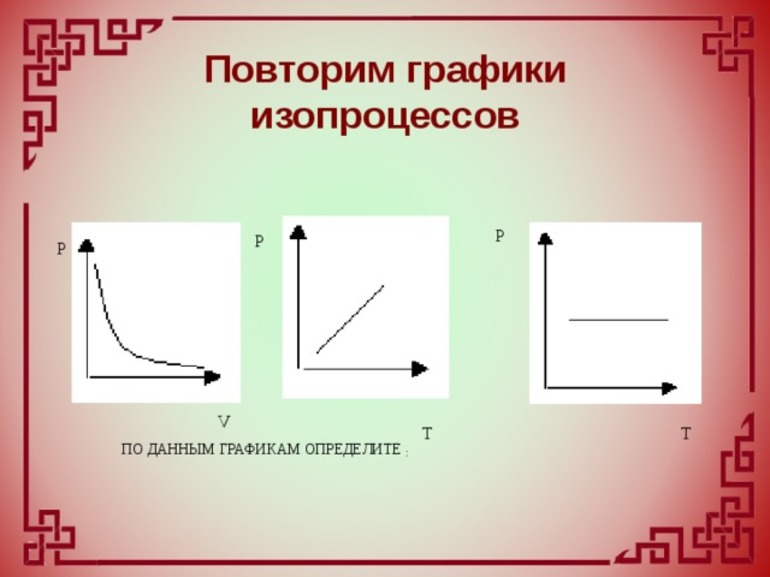
Изопроцессы

С помощью уравнения объединённого газового закона можно исследовать процессы, в которых масса газа и один из важнейших параметров — давление, температура или объём — остаются постоянными. В физике такие процессы называются изопроцессами.

Из объединённого газового закона вытекают другие важнейшие газовые законы: закон Бойля-Мариотта, закон Гей-Люссака, закон Шарля, или второй закон Гей-Люссака.

Изотермический процесс

Процесс, в котором изменяются давление или объём, но температура остаётся постоянной, называется изотермическим процессом.

При изотермическом процессе T = const, m = const.

Поведение газа в изотермическом процессе описывает закон Бойля-Мариотта. Этот закон открыли экспериментальным путём английский физик Роберт Бойль в 1662 г. и французский физик Эдм Мариотт в 1679 г. Причём сделали они это независимо друг от друга. Закон Бойля-Мариотта формулируется следующим образом: В идеальном газе при постоянной температуре произведение давления газа на его объём также постоянно.

Уравнение Бойля-Мариотта можно вывести из объединённого газового закона. Подставив в формулу Т = const,получаем

p·V = const

Это и есть закон Бойля-Мариотта. Из формулы видно, что давление газа при постоянной температуре обратно пропорционально его объёму. Чем выше давление, тем меньше объём, и наоборот.

Как объяснить это явление? Почему же при увеличении объёма газа его давление становится меньше?

Так как температура газа не меняется, то не меняется и частота ударов молекул о стенки сосуда. Если увеличивается объём, то концентрация молекул становится меньше. Следовательно, на единицу площади придётся меньшее количество молекул, которые соударяются со стенками в единицу времени. Давление падает. При уменьшении объёма число соударений, наоборот, возрастает. Соответственно растёт и давление.

Графически изотермический процесс отображают на плоскости кривой, которую называют изотермой. Она имеет форму гиперболы.

Каждому значению температуры соответствует своя изотерма. Чем выше температура, тем выше расположена соответсвующая ей изотерма.

Изобарный процесс

Процессы изменения температуры и объёма газа при постоянном давлении, называются изобарными. Для этого процесса m = const, P = const.

Зависимость объёма газа от его температуры при неизменяющемся давлении также была установлена экспериментальным путём французским химиком и физиком Жозефом Луи Гей-Люссаком, опубликовавшем его в 1802 г. Поэтому её называют законом Гей-Люссака «При постоянном давлении отношение объёма постоянной массы газа к его абсолютной температуре является постоянной величиной».

При Р = const уравнение объединённого газового закона превращается в уравнение Гей-Люссака.

Пример изобарного процесса — газ, находящийся внутри цилиндра, в котором перемещается поршень. При повышении температуры растёт частота ударов молекул о стенки. Увеличивается давление, и поршень приподнимается. В итоге увеличивается объём, занимаемый газом в цилиндре.

Графически изобарный процесс отображается прямой линией, которая называется изобарой.

Чем больше давление в газе, тем ниже расположена на графике соответствующая изобара.

Изохорный процесс

Изохорным, или изохорическим, называют процесс изменения давления и температуры идеального газа при постоянном объёме.

Для изохорного процесса m = const, V = const.

Представить такой процесс очень просто. Он происходит в сосуде фиксированного объёма. Например, в цилиндре, поршень в котором не двигается, а жёстко закреплён.

Изохорный процесс описывается законом Шарля: «Для данной массы газа при постоянном объёме его давление пропорционально температуре». Французский изобретатель и учёный Жак Александр Сезар Шарль установил эту зависимость с помощью экспериментов в 1787 г. В 1802 г. её уточнил Гей-Люссак. Поэтому этот закон иногда называют вторым законом Гей-Люссака.

При V = constиз уравнения объединённого газового закона получаем уравнение закона Шарля, или второго закона Гей-Люссака.

При постоянном объёме давление газа увеличивается, если увеличивается его температура.

На графиках изохорный процесс отображается линией, которая называется изохорой.

Чем больше объём занимаемый газом, тем ниже расположена изохора, соответствующая этому объёму.

В реальности ни один параметр газа невозможно поддерживать неизменным. Это возможно сделать лишь в лабораторных условиях.

Конечно, в природе идеального газа не существует. Но в реальных разреженных газах при очень низкой температуре и давлении не выше 200 атмосфер расстояние между молекулами намного превышает их размеры. Поэтому их свойства приближаются к свойствам идеального газа.

Особенности, каким уравнением выражается

Соотношение, при котором определяется связь параметров состояния друг с другом, называется уравнением состояния данного тела. В самом простом случае равновесное состояние тела определяется значением следующих параметров:

• давления (p);
• объема (V);
• температуры.

Масса тела или системы, как правило, известна.

Существует эквивалентная макроскопическая формулировка идеального газа — это такой газ, который одновременно будет подчиняться закону Бойля-Мариотта и Гей-Люссака. 

Уравнение Менделеева-Клапейрона

Термические свойства классического и квазиклассического идеального газа описываются уравнением состояния идеального газа, которое называется уравнением Менделеева-Клапейрона.

Также уравнение Клапейрона-Менделеева можно записать в ином виде:

§ 5. Уравнение состояния идеального газа

Выясним, как связаны между собой макроскопические параметры идеального газа, которые характеризуют его равновесное состояние: давление, масса всего газа, объём, предоставленный ему, и температура.

Состояние макроскопической системы полностью определено, если известны её макроскопические параметры — давление , масса , температура  и объём . Уравнение, связывающее параметры данного состояния, называют уравнением состояния системы. Изменение параметров состояния системы с течением времени называют процессом.

Если при переходе идеального газа из одного состояния в другое число его молекул  остаётся постоянным, т. е. масса и молярная масса газа не изменяются, то из уравнений  и  следует:

,  ,

(5.1)

где  — постоянная Больцмана;  — параметры начального состояния газа, а  — конечного. Из соотношений (5.1) следует, что

,

или

. 

(5.2)

При неизменных массе и молярной массе идеального газа отношение произведения его давления и объёма к абсолютной температуре является величиной постоянной.

Уравнение (5.2) связывает два рассматриваемых состояния идеального газа независимо от того, каким образом газ перешёл из одного состояния в другое.

Уравнение состояния в виде (5.2) впервые вывел в 1834 г. французский физик Бенуа Клапейрон (1799–1864), поэтому его называют уравнением Клапейрона.

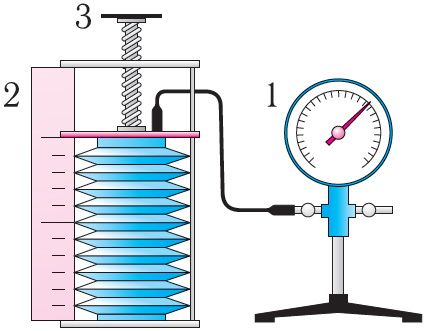Рис. 18

В справедливости уравнения состояния можно убедиться, воспользовавшись установкой, изображённой на рисунке 18. Манометром 1, соединённым с герметичным гофрированным сосудом, регистрируют давление газа внутри сосуда. Объём газа в сосуде можно рассчитать, используя линейку 2. Температура газа в сосуде равна температуре окружающей среды и может быть измерена термометром.

Измерив параметры газа  в начальном состоянии, вычисляют отношение . Затем помещают сосуд в горячую воду. При этом температура газа и его давление изменяются. Вращая винт 3, изменяют вместимость сосуда. Измерив снова давление газа  и температуру , а также рассчитав предоставленный ему объём , вычисляют отношение  Как показывают расчёты, уравнение состояния (5.2) выполняется в пределах погрешности эксперимента.

Уравнение состояния (5.2) можно применять для газов при следующих условиях:

1) не очень большие давления (пока собственный объём всех молекул газа пренебрежимо мал по сравнению с предоставленным ему объёмом);

2) не слишком низкие или же высокие температуры (пока абсолютное значение потенциальной энергии межмолекулярного взаимодействия пренебрежимо мало по сравнению с кинетической энергией теплового движения молекул).

От теории к практике

Рис. 19

На рисунке 19 представлен график процесса перехода идеального газа данной массы из состояния 1 в состояние 2. Как изменился объём газа в результате этого процесса?

Поскольку число частиц , то из уравнения (5.1) следует:

.

(5.3)

Величину, равную произведению постоянной Больцмана  и постоянной Авогадро , назвали универсальной газовой постоянной :

.

(5.4)

С учётом выражения (5.4) уравнение (5.3) примет вид:

. 

(5.5)

Поскольку количество вещества , то формулу (5.5) можно записать в виде:

.

Уравнение состояния в виде (5.5) впервые получил русский учёный Д. И. Менделеев (1834–1907) в 1874 г., поэтому его называют уравнением Клапейрона–Менделеева.

Отметим, что уравнение Клапейрона–Менделеева связывает между собой макроскопические параметры конкретного состояния идеального газа. Используя уравнение Клапейрона–Менделеева, можно описать различные процессы, происходящие в идеальном газе.

Основное уравнение МКТ

Основная задача молекулярно-кинетической теории газа заключается в том, чтобы установить соотношение между давлением газа и его микроскопическими параметрами: массой молекул, их средней скоростью и концентрацией. Это соотношение называется основным уравнением молекулярно-кинетической теории газа или кратко — основным уравнением МКТ.

В основе молекулярно-кинетической теории лежат три положения.

1. Все вещества образованы из мельчайших частиц — молекул, которые состоят из атомов.

   Молекулы химического вещества могут быть простыми и сложными, то есть состоять из одного или нескольких атомов. Молекулы и атомы представляют собой электрически нейтральные частицы. При определенных условиях молекулы и атомы могут приобретать дополнительный электрический заряд и превращаться в положительные или отрицательные ионы.

2. Атомы и молекулы находятся в непрерывном хаотическом движении.
3. Частицы взаимодействуют друг с другом силами, которые имеют электрическую природу. Гравитационное взаимодействие между частицами пренебрежимо мало.

Мы уже выяснили, что причина давления газа на стенки — это удары молекул. Давление напрямую зависит от количества молекул — чем их больше, тем больше ударов о стенки и тем больше давление. А количество молекул в единице объема — это концентрация. Значит, давление газа зависит от концентрации.

Также давление пропорционально квадрату скорости, так как чем больше скорость молекулы, тем чаще она бьется о стенку сосуда. Расчеты показывают, что основное уравнение молекулярно-кинетической теории для идеального газа имеет следующий вид.

Основное уравнение МКТ p = nkT или p — давление газа n — концентрация T — температура газа m — масса одной молекулы v — средняя квадратичная скорость [м/с]

Коэффициент 1/3 обусловлен трехмерностью пространства: во время хаотического движения молекул все три направления равноправны.

Важный нюанс: средняя квадратичная скорость сама по себе не в квадрате! Ее формула указана выше, а в основном уравнении МКТ (да и не только в нем) она возведена в квадрат. Это значит, что формулу средней квадратичной скорости нужно подставлять не вместо v2, а вместо v— и потом уже возводить эту формулу в квадрат. Это часто провоцирует путаницу.

Мы знаем, что кинетическая энергия вычисляется по следующей формуле:

Кинетическая энергия Ек = mv2/2 Ек — кинетическая энергия m — масса тела v — скорость [м/с]

Для молекулы газа формула примет вид:

Средняя кинетическая энергия поступательного движения молекулы Ек = mv2/2 Ек — средняя кинетическая энергия поступательного движения молекулы m — масса молекулы v — скорость молекулы [м/с]

Из этой формулы можно выразить mv2 и подставить в основное уравнение МКТ. Подставим и получим, что давление идеального газа пропорционально произведению концентрации молекул на среднюю кинетическую энергию поступательного движения молекулы.

Основное уравнение МКТ p — давление газа n — концентрация E — средняя кинетическая энергия поступательного движения молекулы

Первое начало термодинамики. Формулы для изопроцессов

Напомним Вам, что первый закон термодинамики гласит: количество теплоты, переданное газу, идёт на изменение внутренней энергии газа U и на совершение газом работы A. Формула первого закона термодинамики записывается так:

Как известно, с газом что-то происходит, мы можем сжать его, можем нагреть. В данном случае нас интересуют такие процессы, которые протекают при одном постоянном параметре. Рассмотрим, как выглядит первое начало термодинамики в каждом из них.

Кстати! Для всех наших читателей сейчас действует скидка 10% на любой вид работы. 

Изотермический процесс протекает при постоянной температуре. Тут работает закон Бойля-Мариотта: в изотермическом процессе давление газа обратно пропорционально его объёму. В изотермическом процессе:

Изохорный процесс протекает при постоянном объеме. Для этого процесса характерен закон Шарля: При постоянном объеме давление прямо пропорционально температуре. В изохорном процессе все тепло, подведенное к газу, идет на изменение его внутренней энергии.

Изобарный процесс идет при постоянном давлении. Закон Гей-Люссака гласит, что при постоянном давлении газа его объём прямо пропорционален температуре. При изобарном процессе тепло идет как на изменение внутренней энергии, так и на совершение газом работы.

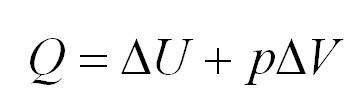
Адиабатный процесс. Адиабатный процесс – это такой процесс, который проходит без теплообмена с окружающей средой. Это значит, что формула первого закона термодинамики для адиабатного процесса выглядит так:

Дополнительные процессы

На практических занятиях по физике проводятся опыты с адиабатным или адиабатическим процессом (изоэнтропийный), связанным с термодинамикой. В явлении нет теплообмена с внешней средой. Чтобы наблюдать за общим случаем всех вышеописанных процессов, используется газ постоянной теплоёмкостью. Явление называется политропическим.

Если давление и температура составных компонентов одинаково, при этом они взяты в равных объёмах, тогда в используемых идеальных газах содержится одно число молекул. На долю одного моля разных веществ приходится N A =6,02·10 23молекул. Это считается числом Авогадро.

По закону Дальтона, давление смеси равно сумме парциальных P, входящих в состав. Выражение записывается следующим образом: P cm=P1+P2+…Pn. Последний показатель Pn является давлением газа, который бы занимал весь объёмом сосуда.

Чаще в старших классах физике рассматриваются изохорические процессы, когда переходит идеальный газ из одного состояния в другое, при этом не изменяется его объёмом. Явление впервые рассмотрел француз Жак Шарль. Закон записывается следующим образом: PV=vRT. Так как v= const и V=const, поэтому для любых разных состояний веществ используется равенство: P1/T1=P2/T2=….Pn/Tn. Закон Шарля математически записывается так: P/T=const.

Из выражения следует, что между температурой и давлением наблюдается прямо пропорциональная связь. Если увеличивается P, тогда повышается T, и наоборот. График зависимости данных величин называется изохорой. На промежутке абсолютного нуля для кривых предусмотрена условная зависимость. Прямая доводится до начала координат с помощью пунктирных линий.

Подобная зависимость T от P и V при изобарных и изохорных процессах определяет точность и эффективность измерения температуры газовыми термометрами. Первыми ученые открыли эти явления, которые считаются частными случаями уравнения состояния. Позже физики утвердили закон Клапейрона и Менделеева.

Если следовать хронологии, сначала изучались процессы, которые протекали при постоянной температуре, а затем при одном объеме. Последними рассматривались изобарические процессы. Редким и интересным явлением считается изоэнтропия, когда изменяется термодинамическая система при условии постоянной энтропии. Последнее записывается как S=const.

Макропараметры

Макропараметры — это параметры, характеризующие систему в целом. Например, объем V, давление p, средняя скорость молекул \(~\left\langle \upsilon
\right\rangle\), температура T, концентрация n и т.д. Значения этих параметров могут быть установлены с помощью измерительных приборов.

Объем газа V — это объем сосуда, в котором газ находится. В Си измеряется в м3. Часто используется несистемная единица измерения 1 литр: 1 л = 10-3 м3.

Давление р — скалярная физическая величина, равная отношению силы F к значению площади S площадки, на которую эта сила действует\. Газ оказывает давление вследствие столкновений молекул со стенками сосуда. В Си единица давления 1 Н/м2 = 1 Па (Паскаль). Внесистемные единицы измерения — 1 мм.рт.ст и 1 атмосфера. Нормальное давление равно одной физической атмосфере. 1 физическая атмосфера = 1 атм = 760 мм.рт.ст, 1 техническая атмосфера = 1 ат = 736 мм.рт.ст. 1 мм.рт.ст. = 133Па.

Более строгое определение давления: давление р — скалярная физическая величина, равная отношению проекции силы на направление нормали к площадке, на которую сила действует, к значению площади этой площади.

Концентрация молекул n — это число молекул N в единице объема, т.е. \(~n = \dfrac{N}{V}\). Измеряется в 1/м3 = м–3.

Температура — скалярная физическая величина, характеризующий степень нагретости тела.

По шкале Цельсия температура обозначается буквой t, измеряется в градусах Цельсия (ºС). За 1 ºС принята одна сотая промежутка от температуры плавления льда (0 ºС) до температуры кипения воды (100 ºС).

Абсолютная температурная шкала — шкала температур, в которой за начало отсчета принят абсолютный нуль. Температура здесь обозначается буквой T, измеряется в кельвинах (К). За единицу измерения в этой шкале принят один градус Цельсия, т.е. изменение на один кельвин (1 К) равно изменению на один градус Цельсия.

T = (t + 273) К или t = (T – 273) ºС,

где T — абсолютная термодинамическая температура (К); t — температура по шкале Цельсия (ºС).

Средние скорости молекул газов

Движение молекул газа подчиняется законам статистической физики. В каждый момент времени скорости отдельных молекул могут значительно отличаться друг от друга, но их средние значения одинаковы и при расчетах используются не мгновенные скорости отдельных молекул, а не которые средние значения. Различают среднюю арифметическую \(~
\left\langle \upsilon \right\rangle\) и среднюю квадратичную \(~\left\langle \upsilon_{KB} \right\rangle\) скорости хаотического движения молекул.

Пусть имеется N молекул, скорости которых соответственно υ₁, υ₂, …, υ_N. Средняя арифметическая скорость хаотического движения молекул (при грубом приближении) по модулю определяется как сумма модулей скоростей молекул газа, деленная на их общее число:

\(~\left\langle \upsilon \right\rangle = \dfrac{\upsilon_1 + \upsilon_2 + \ldots + \upsilon_N}{N} .\)

Средняя квадратичная скорость хаотического движения молекул

\(~\left\langle \upsilon_{KB} \right\rangle = \sqrt{\left\langle \upsilon^2 \right\rangle} = \sqrt{\dfrac{\upsilon^2_1 + \upsilon^2_2 + \ldots + \upsilon^2_N}{N}} ,\)

где \(~\left\langle \upsilon^2 \right\rangle\) — средний квадрат скорости движения молекул. Его не следует смешивать с квадратом средней скорости\.

Как показывают расчеты, \(~\left\langle \upsilon \right\rangle = \sqrt{\dfrac{8R \cdot T}{\pi M}}\); \(~\left\langle \upsilon_{KB} \right\rangle = \sqrt{\dfrac{3R \cdot T}{M}}\) , где R — универсальная газовая постоянная, Μ — молярная масса.

Более строгое определение средней скорости дано тут.

Термодинамические потенциалы

Выражая энтропию как функцию T , V и N :

SkNзнак равнопер⁡(VТc^VNΦ){\ displaystyle {\ frac {S} {kN}} = \ ln \ left ({\ frac {VT ^ {{\ hat {c}} _ {V}}} {N \ Phi}} \ right)}

Химический потенциал идеального газа рассчитывается из соответствующего уравнения состояния (см термодинамического потенциала ):

μзнак равно(∂г∂N)Т,п{\ displaystyle \ mu = \ left ({\ frac {\ partial G} {\ partial N}} \ right) _ {T, P}}

где G — свободная энергия Гиббса и равна U + PV — TS, так что:

μ(Т,п)знак равноkТ(c^п-пер⁡(kТc^ппΦ)){\ displaystyle \ mu (T, P) = kT \ left ({\ hat {c}} _ {P} — \ ln \ left ({\ frac {kT ^ {{\ hat {c}} _ {P}) }} {P \ Phi}} \ right) \ right)}

Химический потенциал обычно соотносится с потенциалом при некотором стандартном давлении P o, так что при :
μо(Т)знак равноμ(Т,по){\ displaystyle \ mu ^ {o} (T) = \ mu (T, P ^ {o})}

μ(Т,п)знак равноμо(Т)+kТпер⁡(ппо){\ displaystyle \ mu (T, P) = \ mu ^ {o} (T) + kT \ ln \ left ({\ frac {P} {Po}} \ right)}

Для смеси ( j = 1,2, …) идеальных газов, каждый из которых имеет парциальное давление P _j , можно показать, что химический потенциал μ _j будет задан приведенным выше выражением с заменой давления P на P _j .

Термодинамические потенциалы идеального газа теперь могут быть записаны как функции от T , V и N как:

Что такое идеальный газ

Уравнение состояния так называемого идеального газа является простым, но достаточно информативным.

Определение 2

Идеальный газ – это газ, в котором пренебрегают взаимодействием молекул между собой.

Идеальными считают разреженные газы. Особенно близки к идеальным газы гелий и водород. Идеальный газ – это упрощенная математическая модель реального газа: молекулы движутся хаотически, а соударения между молекулами и удары молекул о стенки сосуда упругие, не приводящие к потерям энергии в системе. Подобная упрощенная модель весьма удобна, поскольку не требует учета силы взаимодействия между молекулами газа. Множество реальных газов не отличаются в своем поведении от идеального газа в условиях, когда суммарный объем молекул пренебрежимо мал в сравнении с объемом сосуда (то есть при атмосферном давлении и комнатной температуре). Это дает возможность применять уравнение состояния идеального газа для сложных расчетов.

Уравнение состояния идеального газа запишем несколько раз (2), (3), (5):

pV=mμRT=νRT (2).

Уравнение (2) – уравнение Менделеева-Клапейрона, где m – это масса газа, μ – это молярная масса газа, R=8,31 Джмоль·К – это универсальная газовая постоянная, ν – это число молей вещества.

pV=NkT (3),

где N – это количество молекул газа в массе m, k=1,38·10-23 ДжК, постоянная Больцмана, определяющая «долю» газовой постоянной, которая приходится на 1 молекулу и

N=mNAμ (4),

NA=6,02·1023 моль-1 – это постоянная Авогадро.

Если поделить в (4) обе части на V, то получаем следующий вид записи уравнения состояния идеального газа:

p=nkT (5),

где n=NV – это количество частиц в единице объема или же концентрация частиц.

Низкое давление газа параметры

1
1. Давление подключения природного газа

При выборе мощности котла необходимо учесть давление подводимого природного газа в местной газораспределительной сети. Это обусловлено рядом причин и в первую очередь снижением мощности котла при понижении давления (расхода) газа ниже расчетного (указанного в технических характеристиках котла), что не позволяет работать котлу в полном соответствии с его номинальной тепловой мощностью когда это необходимо. Самое неприятное что при сильных морозах, когда собственно и нужно задействовать всю мощность котла, снижается давление в газовых сетях из-за естественного увеличения расхода газа его потребителями. Помимо этого, газопроводы низкого давления были построены в расчете на меньшее количество потребителей газа и несколько другой тип эксплуатируемого газового оборудования. В среднем давление в вышеуказанных газопроводах (например в Московской области) не более 15 мбар (0,0015 Мпа). Исключение составляют некоторые коттеджные поселки с собственными ГРС, газоснабжение которых осуществляется от магистральных газопроводов.

Котельное оборудование практически всех зарубежных (в частности немецких) производителей расчитано по номинальной мощности на давление природного газа 20 мбар. Если давление газа ниже, риск “замерзнуть” в сильные морозы можно уменьшить – внести поправку на давление газа при выборе мощности котла. Совершенно точных расчетов зависимости мощности газоиспользующего оборудования от давления газа нет, но примерную корректировку можно произвести по ниже приведенной формуле.

2
2. Расчет падения тепловой мощности котла при уменьшении давления газа

Q факт. (%) = ( Корень квадратный из ( Р факт. / Р номин.) ) х 100

Q факт. (%) – фактическая тепловая мощность котла, при фактическом давлении газа ниже указанного в техническом паспорте изготовителя (давления, обеспечивающего номинальную тепловую мощность работающего котла);

Р факт. – фактическое давление газа на входе в горелку при работающем котле;

Р номин. – давление газа , указанное в паспорте котла.

При Р факт. = 10 мбар

Р номин. = 20 мбар

Q факт. (%) = (корень квадратный ( 10 /20 ) ) х 100 = 69%

Фактическая тепловая мощность котла составляет 69 % от номинальной тепловой мощности.

3
3 . Газовые горелки с поддувом (вентиляторные)

При выборе горелки с поддувом для комбинированных котлов важно учесть диаметр газовой арматуры для горелки т.к. при достаточно высоком давлении газа можно приобрести горелку с арматурой меньшего диаметра (стоимость горелки в том числе зависит от диаметра газовой арматуры) и соответственно при невысоком давлении – выбрать с арматурой большего диаметра, тем самым обеспечив необходимый расход газа

Подбор вентиляторных горелок осуществляется по таблицам технической документации производителей. Во всех случаях подводящий газопровод к горелке целесообразно выполнить большего диаметра т.к. это уменьшит риск возникновения сбоев в работе котла и снижения его мощности при сезонных колебаниях давления (расхода) в газораспределительных сетях.