Теплоемкость

Работа в термодинамике

Работа в термодинамике равна изменению внутренней энергии тела.

Обозначение работы газа – ​\( A’ \)​, единица измерения в СИ – джоуль (Дж). Обозначение работы внешних сил над газом – ​\( A \)​.

Работа газа ​\( A’ =-A \)​.

Работой расширения идеального газа называют работу, которую газ совершает против внешнего давления.

Работа газа положительна при расширении и отрицательна при его сжатии. Если объем газа не изменяется (изохорный процесс), то работы газ не совершает.

Графически работа газа может быть вычислена как площадь фигуры под графиком зависимости давления от объема в координатных осях ​\( (p,V) \)​, ограниченная графиком, осью ​\( V \)​ и перпендикулярами, проведенными из точек начального и конечного значений объема.

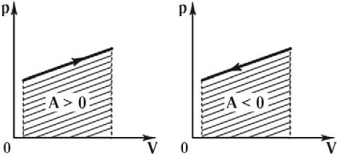
Формула для вычисления работы газа:

в изобарном процессе ​\( A’=p\cdot\Delta V. \)​

в изотермическом процессе \( A’=\frac{m}{M}RT\ln\frac{V_2}{V_1}. \)​

Ссылки [ править ]

1. ^ Открытый университет (2008). S104 Книга 3 Энергия и свет , стр. 59. Открытый университет . ISBN  9781848731646 .
2. ^ Нейв, Р. «Удельная теплоемкость» . Гиперфизика . Государственный университет Джорджии . Проверено 18 февраля 2010 .
3. ^ Открытый университет (2008). S104 Книга 3 Энергия и свет , стр. 179. Открытый университет . ISBN 9781848731646 . 
4. ^ Engineering ToolBox (2003). «Удельная теплоемкость некоторых обычных веществ» .
5. ^ (2001): Колумбийская энциклопедия , 6-е изд .; цитируется Encyclopedia.com . Издательство Колумбийского университета. Проверено 11 апреля 2019 г.
6. ^ Laidler, Кейт, J. (1993). Мир физической химии . Издательство Оксфордского университета. ISBN 0-19-855919-4.
7. ^ Международное бюро мер и весов (2006), Международная система единиц (СИ) (8-е изд.), ISBN  92-822-2213-6, архивировано из оригинала на 2017-08-14
8. ^ «Вода — тепловые свойства» . Engineeringtoolbox.com . Проверено 31 октября 2013 .
9. ^ Международный союз чистой и прикладной химии, Отдел физической химии. «Величины, единицы и символы в физической химии» . Blackwell Sciences. п. 7. Прилагательное «специфический» перед названием обширного количества часто используется для обозначения деления по массе.
10. ^ Справочник Ланге по химии, 10-е изд. стр. 1524
11. ^ Быстрый, CR; Schawe, JEK; Угговицер, П.Дж.; Погатчер, С. (01.07.2019). «Измерение удельной теплоемкости с помощью быстрой сканирующей калориметрии — точность и корректировка потерь» . Thermochimica Acta . Спецвыпуск к 65-летию Кристофа Шика. 677 : 12–20. DOI10.1016 / j.tca.2019.03.021 . ISSN 0040-6031 .
12. ^ Pogatscher, S .; Leutenegger, D .; Schawe, JEK; Угговицер, П.Дж.; Леффлер, Дж. Ф. (сентябрь 2016 г.). «Фазовые переходы твердое тело – твердое тело при плавлении в металлах» . Nature Communications . 7 (1): 11113. Bibcode2016NatCo … 711113P . DOI10.1038 / ncomms11113 . ISSN 2041-1723 . PMC 4844691 . PMID 27103085 .
13. ^ Кох, Вернер (2013). Таблицы VDI Steam (4-е изд.). Springer. п. 8. ISBN 9783642529412.Издается под эгидой Verein Deutscher Ingenieure (VDI).
14. ^ Кардарелли, Франсуа (2012). Преобразование научных единиц: Практическое руководство по метрике . MJ Shields (перевод) (2-е изд.). Springer. п. 19. ISBN 9781447108054.
15. Перейти ↑ Feynman, R., The Feynman Lectures on Physics , Vol. 1, гл. 40, стр. 7–8
16. ^ Райф, F. (1965). Основы статистической и теплофизики . Макгроу-Хилл. С.  253–254 .
17. ^ Киттель, Чарльз и Кремер, Герберт (2000). Теплофизика . Фримен. п. 78. ISBN 978-0-7167-1088-2.
18. ^ Торнтон, Стивен Т. и Рекс, Эндрю (1993) Современная физика для ученых и инженеров , издательство Saunders College Publishing
19. ^ Chase, MWмладший (1998) NIST-JANAF Themochemical таблицы, четвертое издание , в Журнал физических и химических справочных данных , монография 9, стр 1-1951.
20. ^ Фейнман, Ричард Фейнман Лекции по физике , Vol. 1, гл. 45
21. ^ Cengel, Юнус А. и Boles, Майкл А. (2010) Термодинамика: инженерный подход , 7е издание, McGraw-Hill ISBN 007-352932-X . 

Идеальный газ

Идеальный газ – это идеализация, как и материальная точка. Молекулы такого газа являются материальными точками, а соударения молекул – абсолютно упругие. Взаимодействием же молекул на расстоянии пренебрегаем. В задачах по термодинамике реальные газы часто принимаются за идеальные. Так гораздо легче жить, и не нужно иметь дела с массой новых членов в уравнениях.

Итак, что происходит с молекулами идеального газа? Да, они движутся! И резонно спросить, с какой скоростью? Конечно, помимо скорости молекул нас интересует еще и общее состояние нашего газа. Какое давление P он оказывает на стенки сосуда, какой объем V занимает, какая у него температура T.

Для того, чтобы узнать все это, есть уравнение состояния идеального газа, или уравнение Клапейрона-Менделеева

Здесь m – масса газа, M – его молекулярная масса (находим по таблице Менделеева), R – универсальная газовая постоянная, равная 8,3144598(48) Дж/(моль*кг).

Универсальная газовая постоянная может быть выражена через другие константы (постоянная Больцмана и число Авогадро)

Массу, в свою очередь, можно вычислить, как произведение плотности и объема.

Физика для средней школы

Теплоемкости при постоянном давлении и постоянном объеме

При сообщении телу некоторого количества теплоты изменяется его температура (за исключением агрегатных превращений и вообще изотермических процессов). Характеристиками такого изменения являются различные теплоемкости: теплоемкость тела , удельная теплоемкость вещества c, молярная теплоемкость C.

Понятия теплоемкости тела и удельной теплоемкости рассмотрены тут.

Молярная теплоемкость C — величина, равная количеству теплоты, необходимому для нагревания 1 моль вещества на 1 К:

Единицей молярной теплоемкости в СИ является джоуль на моль-Кельвин (Дж/моль·К).

Удельная теплоемкость связана с молярной соотношением

C = cM.

В отличие от такой, например, характеристики вещества, как его молекулярная масса Mr удельная теплоемкость вещества не является неизменным параметром. Удельная теплоемкость может резко изменяться при переходе вещества из одного агрегатного состояния в другое. Так, вода в газообразном состоянии имеет удельную теплоемкость а в жидком .

Теплоемкость зависит и от условий, при которых происходит передача теплоты телу. Последнее особенно относится к газам. Например, при изотермическом расширении газа ему передается некоторое количество теплоты . Следовательно, удельная теплоемкость газа при изотермическом процессе

При адиабатном сжатии (расширении) газ не получает теплоты и не передает ее окружающим телам (Q = 0), а температура газа изменяется . Следовательно, удельная теплоемкость газа при адиабатном процессе

Наибольший интерес представляет теплоемкость для случаев, когда нагревание происходит при постоянном объеме или при постоянном давлении. В первом случае теплоемкость называется теплоемкостью при постоянном объеме или изохорной теплоемкостью , во втором — теплоемкостью при постоянном давлении или изобарной теплоемкостью .

Если объем не изменяется , то работа, совершенная газом, так же равна нулю (А = 0). Согласно первому закону термодинамики

Откуда

Следовательно, теплоемкость при постоянном объеме равна изменению внутренней энергии газа при изменении температуры на 1 К.

Если газ идеальный, то в формуле (2)

Тогда молярная теплоемкость при постоянном объеме

— изменение внутренней энергии 1 моль газа. Из этих равенств теплоемкость газа при постоянном объеме —

молярная теплоемкость газа при постоянном объеме —

Если газ нагревается при постоянном давлении, то согласно первому закону термодинамики

где

Тогда теплоемкость газа при постоянном давлении

Молярная теплоемкость при постоянном давлении:

Таким образом, теплоемкость при постоянном давлении всегда больше теплоемкости при постоянном объеме. Их отношение равно

где — показатель адиабаты (коэффициент Пуассона).

Из-за малости величины коэффициента объемного расширения твердых и жидких тел работой, совершаемой ими при нагревании при постоянном давлении, можно пренебречь и считать, что теплоемкости при постоянном объеме и постоянном давлении практически совпадают. Поэтому теплоемкость твердых и жидких тел при заданной температуре может считаться вполне определенной величиной.

Удельная теплоемкость газов и паров (таблица)

Значения при постоянном давлении относятся обычно к атмосферному давлению.

Газ	Температура	Удельная теплоемкость
Азот 1)	0,732
Аргон	0—2 000	0,3122
Водород 2)	ок. 50	10,05
Воздух 3)	0,718
Окись углерода СО	1000	0,950
Окись углерода СО	1800	1,002
Пары воды	100	1,463
Углекислый газ 4)	ок. 55	0,691
Азота закись N3O	26—103	0,892
Азота окись NO	13—171	0,971
Азота перекись NO2	27—67	0,680
Аргон	15	0,523
Воздух (сухой)	20	1,006
Воздух (сухой)	100	1,011
Воздух (сухой)	500	1,092
Воздух (сухой)	1000	1,192
Воздух (сухой)	—100	1,008
Воздух (сухой) (100 атм)	—80	1,902
Сероуглерод CS2	86—190	0,670
Скипидар C10H1	179—249	2,118
Спирт метиловый СН2O	101—223	1,917
Хлороформ СНСl3	27—118	0,603
Эфир этиловый (C2H5)2O	25—111	1,791
1) Для N сv = 0,732 + 0,00067t, t обозначает темпера­туру. 2) Для Н cv уменьшается с увеличением плотности и понижением температуры. 3) Для воздуха cv = 0,7184 + 0,1167р, где р обозначает плотность (г/мл). 4) Для СО2, cv= 0,691 + 0,889Р + 1,42р2.

Второй закон термодинамики

Все процессы в природе протекают только в одном направлении. В обратном направлении самопроизвольно они протекать не могут. Необратимым называется процесс, обратный которому может протекать только как составляющая более сложного процесса.

Примеры необратимых процессов:

• переход тепла от более нагретого тела к менее нагретому телу;
• переход механической энергии во внутреннюю энергию.

Первый закон термодинамики ничего не говорит о направлении процессов в природе.

Второй закон термодинамики выражает необратимость процессов, происходящих в природе. Существует несколько его формулировок.

Второй закон термодинамики (формулировка Клаузиуса):
невозможно перевести тепло от более холодной системы к более горячей при отсутствии одновременных изменений в обеих системах или окружающих телах.

Второй закон термодинамики (формулировка Кельвина):
невозможно осуществить такой периодический процесс, единственным результатом которого было бы получение работы за счет теплоты, взятой от одного источника.

Эта формулировка говорит также и о том, что невозможно построить вечный двигатель второго рода, то есть двигатель, совершающий работу за счет охлаждения какого-либо одного тела.

Важно!
В формулировке второго закона термодинамики большое значение имеют слова «единственным результатом». Если процессы, о которых идет речь, не являются единственными, то запреты снимаются

Например, в холодильнике происходит передача тепла от более холодного тела к нагретому и при этом осуществляется компенсирующий процесс превращения механической энергии окружающих тел во внутреннюю энергию.

Второй закон термодинамики выполняется для систем с огромным числом частиц. В системах с малым количеством частиц возможны флуктуации – отклонения от равновесия.

Отношение удельных теплоемкостей cp и сv для газов и паров

γ — отношение удельной теплоемкости при постоянном давлении к удельной теплоемкости при постоянном объеме.

Для непосредственного определения γ обычно применяется метод, основанный на адиабатическом расширении газа; для этого можно, например, определять скорость звука в газах. Зная давление или температуру непосредственно после адиабатического расши­рения (метод Клемана и Дезорма и метод Луммера и Прингсхейма), y можно найти из уравнений:

или

Газ	Температура, C	γ
Аргон	1,667
Гелий	1,63
Криптон	19	1,689
Ксенон	19	1,666
Неон	19	1,642
Пары ртути	310	1,666
Азот	20	1,401
Азота окись	—	1,394
Водород	4—17	1,407/8
Кислород	5—14	1,400
Окись углерода	1800	1,297
Воздух (сухой)	—79,3	1,405
Воздух (сухой)	0—17	1,401/2
Воздух (сухой)	500	1,357
Воздух (сухой)	900	1,32
Воздух (сухой) (200 атм)	0 —79,3	1,828 2,333
Азота закись N2O	—	1,324
Азота перекись N2O4	20	1,172
Азота перекись NO2	150	1,31
Аммиак NH3	—	1,336
Озон	—	1,29 1)
Пары воды	100	1,334
Сернистый газ	16—34	1,26
Сернистый газ	500	1,2
Сероводород H2S	—	1,340
Сероуглерод CS2	—	1,239
Углекислый газ	4—11	1,300
Углекислый газ	300	1,22
Углекислый газ	500	1,20
Ацетилен С2Н2	—	1,26
Бензол	20	1,40
Бензол	99,7	1,105
Метан СН4	—	1,313-
Метил бромистый	—	1,274
Метил йодистый	—	1,286
Метил хлористый	19—30	1,279
Пропан С3Н8	—	1,130
Спирт метиловый	99,7	1,256
Спирт этиловый	53	1,133
Спирт этиловый	99,8	1,134
Уксусная кислота	136,5	1,147
Хлороформ СНСl3	24—42 99,8	1,110 1,150
Четыреххлористый углерод СС1	—	1,130
Этан С2Н6	—	1,22
Этил бромистый	—	1,188
Этил хлористый	22,7	1,187
Этилен С2Н4	—	1,264
Эфир этиловый	12—20	1,024
Эфир этиловый	99,7	1,112
1) Экстраполировано

_______________

Источник информации: КРАТКИЙ ФИЗИКО-ТЕХНИЧЕСКИЙ СПРАВОЧНИК/ Том 1, — М.: 1960.

5.7. Адиабатный процесс

Мы
рассмотрели изотермический, изобарный
и изохорный процессы. После ознакомления
с первым законом термодинамики появляется
возможность изучить еще один процесс,—это
процесс, протекающий в системе при
отсутствии теплообмена с окружающими
телами. (Но работу над окружающими телами
система может совершать.)

Процесс в
теплоизолированной системе называют
адиабатным.

При
адиабатном процессе Q=
0 и согласно закону (5.5.3) изменение
внутренней энергии происходит только
за счет совершения работы:

(5.7.1)

Конечно, нельзя
окружить систему оболочкой, абсолютно
исключающей теплообмен. Но в ряде случаев
реальные процессы очень близки к
адиабатным. Существуют оболочки,
обладающие малой теплопроводностью,
например двойные стенки с вакуумом
между ними. Так изготовляются термосы.

Процесс можно
считать адиабатным даже без теплоизолирующей
оболочки, если он происходит достаточно
быстро, т. е. так, чтобы за время процесса
не происходило заметного теплообмена
между системой и окружающими телами.

Согласно
выражению (5.7.1) при совершении над
системой положительной работы, например
при сжатии газа, внутренняя энергия его
увеличивается; газ нагревается. Наоборот,
при расширении газ сам совершает
положительную работу (А’ > 0), но А
0
и внутренняя энергия его уменьшается;
газ охлаждается.

Зависимость
давления газа от его объема при адиабатном
процессе изображается кривой, называемой
адиабатой
(рис. 5.9). Адиабата обязательно идет круче
изотермы. Ведь при адиабатном процессе
давление газа уменьшается не только за
счет увеличения объема, как при
изотермическом процессе, но и за счет
уменьшения его температуры.

Рис. 5.9

Адиабатные процессы
широко используются в технике. Они
играют немалую роль в природе.

Нагревание воздуха
при быстром сжатии нашло применение в
двигателях Дизеля. В этих двигателях
отсутствуют системы приготовления и
зажигания горючей смеси, необходимые
для обычных бензиновых двигателей
внутреннего сгорания. В цилиндр
засасывается не горючая смесь, а
атмосферный воздух. К концу такта сжатия
в цилиндр с помощью специальной форсунки
впрыскивается жидкое топливо (рис.
5.10). К этому моменту температура сжатого
воздуха так велика, что горючее
воспламеняется.

Рис. 5.10

Так как в двигателе
Дизеля сжимается не горючая смесь, а
воздух, то степень сжатия у этого
двигателя больше, а значит, коэффициент
полезного действия (КПД) двигателей
Дизеля выше, чем у обычных двигателей
внутреннего сгорания. Кроме того, они
могут работать на более дешевом
низкосортном топливе. Есть, однако, у
двигателя Дизеля и недостатки:
необходимость высоких степеней сжатия
и большое рабочее давление делают эти
двигатели массивными и вследствие этого
более инерционными — они медленнее
набирают мощность. Двигатели Дизеля
более сложны в изготовлении и эксплуатации,
тем не менее они постепенно вытесняют
обычные бензиновые двигатели, используемые
в автомобилях.

Охлаждение газа
при адиабатном расширении происходит
в грандиозных масштабах в атмосфере
Земли. Нагретый воздух поднимается
вверх и расширяется, так как атмосферное
давление падает с высотой. Это расширение
сопровождается значительным охлаждением.
В результате водяные пары конденсируются
и образуются облака.

Случай твердых тел

Текущие значения

Вещество (твердая фаза)	Масса тепловой мощности ( Й К -1  кг -1 )
Асфальт	1,021
Кирпич	840
Конкретный	880
Гранит	790
Гипс	1,090
Мрамор	880
Песок	835
Стекло	720
Древесина	≈ 1200-2700

Случай кристаллизованных твердых тел

В случае твердых тел при достаточно высокой температуре применим закон Дюлонга и Пти, который позволяет, в частности, обнаружить, что при низкой температуре это происходит благодаря вкладу фононов . Если твердое тело представляет собой металл , мы должны добавить вклад электронов, который пропорционален температуре.
ПРОТИВV∼Т3{\ Displaystyle C_ {V} \ sim T ^ {3}}

Коэффициенты расширения твердых и жидких тел, как правило, достаточно низки, чтобы пренебречь разницей между C _p и C _V для большинства приложений.

Вещество	Θ{\ displaystyle \ Theta}( К )
Al	398
C (ромб)	1860
Cu	315
Fe	420
K	99
Pb	88

Согласно теории Дебая , молярная теплоемкость простого твердого тела может быть определена по формуле:

ПРОТИВV(Т)знак равно3р(4D(ты)-3тыеты-1){\ Displaystyle C_ {V} (T) = 3R \ left (4D (u) — {\ frac {3u} {\ mathrm {e} ^ {u} -1}} \ right)}

с ,
тызнак равноΘТ{\ Displaystyle и = {\ гидроразрыва {\ Theta} {T}}}

Θ{\ displaystyle \ Theta} — температура Дебая, характерная для каждого вещества,

R — молярная постоянная газов ,

и .D(ты)знак равно3ты3∫ты(Икс2+ИксеИкс-1)Икс2dИкс{\ displaystyle D (u) = {\ frac {3} {u ^ {3}}} \ int _ {0} ^ {u} \ left ({\ frac {x} {2}} + {\ frac { x} {\ mathrm {e} ^ {x} -1}} \ right) x ^ {2} \ mathrm {d} x}

Эта формула упрощается как при низкой, так и при высокой температуре; в последнем случае мы находим закон Дюлонга и Пти  :

ПРОТИВV(Т)знак равно{125π4р(ТΘ)3,если Т≪Θ3ресли Т≫Θ{\ Displaystyle C_ {V} (T) = {\ begin {cases} {\ frac {12} {5}} \ pi ^ {4} R \ left ({\ frac {T} {\ Theta}} \ right ) ^ {3}, & {\ text {si}} T \ ll \ Theta \\ 3R & {\ text {si}} T \ gg \ Theta \ end {case}}}

Теория больше не действительна для составных тел.

Эмпирические формулы

Для чистых веществ (твердых, жидких или газообразных) и при постоянном давлении могут быть определены две эмпирические формулы с тремя параметрами для заданного температурного интервала:

ПРОТИВпзнак равнов+бТ+противТ2{\ displaystyle C_ {p} = a + bT + cT ^ {2}}или иначе .ПРОТИВпзнак равнов′+б′Т+против′Т-2{\ displaystyle C_ {p} = a ‘+ b’T + c’T ^ {- 2}}

Значения коэффициентов указаны в таблицах и характерны для данного тела.

Например, для сухой древесины:

противп,внетчасуdрезнак равно0,1031+0,003867Т{\ displaystyle c_ {p, безводный} = 0 {,} 1031 + 0 {,} 003 \, 867 \, T}

с участием:

• противп,внетчасуdре{\ displaystyle c_ {p, безводный}} : выражается в кДж · K −1  кг −1
• T  : термодинамическая температура ( K ).

При 20  ° C для сухой древесины получается 1236 Дж ·  К -1  кг -1 .

Для влажной древесины:

противп,частымяdезнак равно100противп,внетчасуdре+ЧАСsпротивп,евты100+ЧАСs{\ displaystyle c_ {p, wet} = {\ frac {100 \, c_ {p, безводный} + Hs \, c_ {p, вода}} {100 + Hs}}}

где Hs — масса воды по отношению к массе сухой древесины в%.

Уравнение теплового баланса

Если система тел является теплоизолированной, то ее внутренняя энергия не будет изменяться несмотря на изменения, происходящие внутри системы. Если ​\( A \)​ = 0, ​\( Q \)​ = 0, то и ​\( \Delta U \)​ = 0 .

При любых процессах, происходящих в теплоизолированной системе, ее внутренняя энергия не изменяется (закон сохранения внутренней энергии).

Рассмотрим теплоизолированную систему из двух тел с разными температурами. При контакте между ними будет проходить теплообмен. Тело с большей температурой будет отдавать некоторое количество теплоты, а тело с меньшей температурой – получать, пока температуры тел не станут равными. Так как суммарная внутренняя энергия не должна изменяться, то, на сколько уменьшится внутренняя энергия более нагретого тела, на столько должна увеличиться внутренняя энергия второго тела. Так как работа не совершается, то изменение внутренней энергии равно количеству теплоты.

Количество теплоты, отданное при теплообмене телом с большей температурой, равно по модулю количеству теплоты, полученному телом с меньшей температурой:

Другая формулировка: если тела образуют замкнутую систему и между ними происходит только теплообмен, то алгебраическая сумма отданных ​\( Q_{отд} \)​ и полученных \( Q_{пол} \) количеств теплоты равна нулю:

Тепловые машины. Формула КПД в термодинамике

Тепловая машина, в простейшем случае, состоит из нагревателя, холодильника и рабочего тела. Нагреватель сообщает тепло рабочему телу, оно совершает работу, затем охлаждается холодильником, и все повторяется вновь. Типичным примером тепловой машины является двигатель внутреннего сгорания.

Коэффициент полезного действия тепловой машины вычисляется по формуле

Вот мы и собрали основные формулы термодинамики, которые пригодятся в решении задач. Конечно, это не все все формулы из темы термодинамика, но их знание действительно может сослужить хорошую службу. А если возникнут вопросы  – помните о студенческом сервисе, специалисты которого готовы в любой момент прийти на выручку.

Математические упражнения

  Для расчёта теплопотерь и системы отопления своего будущего дома я использовал специализированный программный продукт по расчёту элементов инженерных систем «VALTEC» от некоего ООО «Веста-Трейдинг». Программа VALTEC.PRG находится в открытом доступе и дает возможность рассчитать водяное радиаторное, напольное и настенное отопление, определить теплопотребность помещений, необходимые расходы холодной, горячей воды, объем канализационных стоков, получить гидравлические расчеты внутренних сетей тепло- и водоснабжения объекта. Так вот, используя эту чудесную бесплатную программку я высчитал, что теплопотери моего дома площадью в 152 квадратных метра составляют чуть менее 5 кВт тепловой энергии. В сутки выходит 120 кВт·ч или 432 МДж теплоты. Если допустить, что я буду использовать водяной теплоаккумулятор, который каким-либо источником тепла один раз в сутки разогреется до 85°С и будет постепенно отдавать тепло в систему тёплых полов до температуры 25°С  (ΔT=60 °С), то для накопления 432 МДж теплоты мне потребуется ёмкость m=Q/(C·ΔT),    432/(4,184·60)=1,7 м³.  

      А что было бы, если бы я установил в доме кирпичную печь, например. Разогретый в топке до 500°С кирпич весом в 1 тонну полностью компенсирует теплопотери моего дома в течение суток. При этом объём кирпича будет около 0,5 кубометра. 

    Особенностью моего проекта дома (в общем-то ничего особенного) является отопление тёплым водяным полом. Труба теплоносителя будет заложена в 7-и сантиметровый слой бетонной стяжки под всей площадю пола (152 м²) — это 10,64 м³ бетона! Под бетонной стяжкой планируется деревянное перекрытие по балкам с 25-ю сантиметрами пенополистирольного утеплителя — можно сказать, что через такой пирог утепления 1 м² пола будет терять тепла около 4 Вт, чем, конечно, можно смело пренебреч. Какова же будет теплоёмкость пола? При температуре теплоносителя 27°С бетонная стяжка впитает в себя 580 МДж теплоты, что эквивалентно 161 кВт·ч энергии и с лихвой перекрывает суточную потребность в тепле. Иными словами, зимой при -20°С (именно на такие температуры делался расчёт теплопотерь дома) мне нужно будет раз в два дня подогревать до 27°С пол, а если установить дополнительный водяной теплоаккумулятор на 1000 литров — то и вовсе раза два в неделю будет работать котёл! 

      Вот такая она, теплоёмкость при очень поверхностном рассмотрении. 

Теплоусвоение

  Коэффициент теплоусвоения (англ. U-value) отражает способность материала воспринимать теплоту при колебании температуры на его поверхности или, иными словами, этот коэффициент S показывает способность поверхности материала площадью в 1 м² усваивать теплоту в течение 1 с при температурном перепаде в 1 °С. Как это можно понять из повседневной жизни? Если приложить одновременно обе руки к двум поверхностям из бетона и пенопласта, имеющим одинаковую температуру, то первая будет восприниматься как более холодная — эксперимент ещё со школьных уроков физики. Это ощущение вызывается тем, что бетонная поверхность более интенсивно отбирает (усваивает) тепло от руки, чем пенопластовая, так как бетон имеет больший коэффициент теплоусвоения (Sбетона=18 Вт/(м²·°С), Seps=0,41 Вт/(м²·°С)), не смотря на то, что удельная теплоёмкость пенопласта в полтора раза больше, чем бетона.

   Величина коэффициента теплоусвоения S материалов при периоде колебания теплового потока 24 ч пропорциональна коэффициенту теплопроводности λ, Вт/(м·K), удельной теплоёмкости с, Дж/(кг·K), и плотности материала ρ, кг/м³, и обратно пропорциональна периоду тепловых колебаний T, с (формула слева). Но в строительной практике используются формулы, учитывающие действие массового отношения влаги в материале и климатические условия эксплуатации. Дабы не загромождать вас ненужной инфой, предлагаю использовать уже вычисленные табличные данные из СНиП II-3-79 «Строительная теплотехника». Наиболее интересные я собрал в небольшую табличку.

Первое начало термодинамики. Формулы для изопроцессов

Напомним Вам, что первый закон термодинамики гласит: количество теплоты, переданное газу, идёт на изменение внутренней энергии газа U и на совершение газом работы A. Формула первого закона термодинамики записывается так:

Как известно, с газом что-то происходит, мы можем сжать его, можем нагреть. В данном случае нас интересуют такие процессы, которые протекают при одном постоянном параметре. Рассмотрим, как выглядит первое начало термодинамики в каждом из них.

Кстати! Для всех наших читателей сейчас действует скидка 10% на любой вид работы. 

Изотермический процесс протекает при постоянной температуре. Тут работает закон Бойля-Мариотта: в изотермическом процессе давление газа обратно пропорционально его объёму. В изотермическом процессе:

Изохорный процесс протекает при постоянном объеме. Для этого процесса характерен закон Шарля: При постоянном объеме давление прямо пропорционально температуре. В изохорном процессе все тепло, подведенное к газу, идет на изменение его внутренней энергии.

Изобарный процесс идет при постоянном давлении. Закон Гей-Люссака гласит, что при постоянном давлении газа его объём прямо пропорционален температуре. При изобарном процессе тепло идет как на изменение внутренней энергии, так и на совершение газом работы.

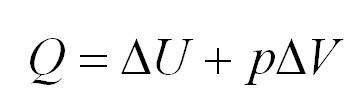
Адиабатный процесс. Адиабатный процесс – это такой процесс, который проходит без теплообмена с окружающей средой. Это значит, что формула первого закона термодинамики для адиабатного процесса выглядит так: