Формула расчета крутящего момента по мощности двигателя

Что такое плечо силы и как его нарисовать

Предположим, нужно с помощью ключа закрутить гайку (см. рис. 2).

Рис. 2. Красная точка, вокруг которой вращается ключ — это центр гайки

Винт, на который накручена гайка – это ось вращения. Ключ может вращаться вокруг красной точки. Для упрощения назовем ее кратко: «точка вращения».

Примечание:

Ось вращения проходит перпендикулярно плоскости рисунка через красную точку. Используем вместо оси вращения термин «точка вращения» для простоты.

Рассмотрим следующий рисунок (см. рис. 3)

Рис. 3. Плечо силы – это перпендикуляр \( l \). Он соединяет линию действия силы с точкой вращения

На рисунке 3 черная стрелка – это вектор силы, которая вращает ключ. Пунктир – линия действия силы. Из красной точки к линии действия силы проведен перпендикуляр. Этот перпендикуляр, обозначенный \( l \), называется плечом силы.

Перпендикуляр к линии действия легко провести с помощью прямоугольного треугольника (см. рис. 4):

Рис. 4. Один катет приложим к линии действия силы, вдоль второго проведем перпендикуляр к точке вращения

Плечо силы проводят так:

1. взять прямоугольный треугольник;
2. приложить один из катетов к линии действия;
3. провести перпендикуляр к точке вращения, используя второй катет;

Что важнее: мощность или крутящий момент для динамики авто

На этом показателе стоит остановить внимание при выборе автомобиля. Если мощность двух ДВС различается несущественно, стоит выбирать самый моментный, особенно если используется механическая коробка переключения передач

Именно этот показатель в промежуточных режимах сыграет ключевую роль. Если мотор всё время будет работать на пределе, мощность ничего не даст. Она важна, но только не при максимальных оборотах. В остальных условиях, двигатели с большим крутящим моментом выиграют.

Зависимость крутящего момента от оборотов двигателя

Для широкого понимания темы нужно углубиться в оба термина и рассмотреть их детали, чтобы понять, чем отличается мощность от крутящего момента. Для этого сравним рабочие характеристики этих показателей:

1. Мощность мотора – это второстепенная рабочая характеристика, она производная крутящего момента;
2. Самый важный показатель работы двигателя внутреннего сгорания – это крутящий момент на коленвале;
3. Частота вращения коленвала определяет мощность мотора. Чем больше обороты, тем выше мощность ДВС (разумеется до определённого потолка);
4. Частота увеличения оборотов мотора повышает крутящий момент, но достигнув максимального значения, КМ уменьшается, независимо от частоты вращения оборотов.
5. Мощность от крутящего момента выражается формулой: N = Мкр *n/9549 (N – мощность, Мкр – крутящий момент, n – количество оборотов коленвала за 1 минуту, 9549 — коэффициент).

Какие выводы из этого можно сделать?

• При выборе автомобиля и сравнивая крутящий момент и мощность, большее значение имеет первый показатель;
• При выборе моторов с идентичными рабочими характеристиками предпочтительнее выбирать ДВС с большим крутящим моментом;
• Чтобы обеспечить лучшую динамику разгона и эффективную тягу мотора, частоту вращения коленвала нужно держать в том диапазоне, при котором крутящий момент достигает своего максимального значения. У одних силовых агрегатов пик крутящего момента достигается при 3000 об./мин., а у других при 4500 об./мин. Чем меньше эти значения, тем быстрее разгоняется машина.

Отмечу, что двигатель выдаст максимум тяги не в одной точке, а в диапазоне – это «полка крутящего момента». Это можно легко заметить при движении авто в гору с механической КПП. Здесь диапазона мощности хватает, чтобы не переходить на низкую передачу, потому что запаса крутящего момента хватит, чтобы тянуть авто в пределах одной передачи. То же самое касается и динамичных манёвров на высокой скорости.

Если крутящий момент можно увеличить в несколько раз, то почему у него есть предел — «потолок», выше которого он не может быть увеличен? Главная характеристика мотора – это мощность, которую никак не изменить. Если водитель выиграет в скорости, то проиграет в крутящем моменте, и наоборот. Хоть это и звучит нелогично, но показатель КМ не должен вообще интересовать автомобилиста, ведь раскрутить мотор можно и при высоком передаточном числе.

Мощность является расчётной величиной, которую нельзя измерить отдельно от крутящего момента, поскольку она от него зависит. Крутящий момент показывает ту мощность, которая будет видна при нажатии педали газа при обгоне. Чем больше момента, тем лучше динамика автомобиля. Мощность просто влияет на максимальную скорость машины.

Динамика вращения

В начале статьи мы записали кинематические характеристики, которые используются для описания движения вращения. В динамике вращения главным уравнением, которое использует эти характеристики, является следующее:

Действие момента M на систему, имеющую момент инерции I, приводит к появлению углового ускорения α.

Данную формулу применяют, для определения угловых частот вращения в технике. Например, зная вращающий момент асинхронного двигателя, который зависит от частоты тока в катушке статора и от величины изменяющегося магнитного поля, а также зная инерционные свойства вращающегося ротора, можно определить, до какой скорости вращения ω раскручивается ротор двигателя за известное время t.

Единицы измерения момента силы

Несколько слов также следует сказать о том, в каких единицах в СИ измеряется вращающий момент. Согласно записанной для него формуле, он измеряется в ньютонах на метр (Н*м). Однако в этих единицах также измеряется работа и энергия в физике (1 Н*м = 1 джоуль). Джоуль для момента M¯ не применяется, поскольку работа является скалярной величиной, M¯ же – это вектор.

Тем не менее совпадение единиц момента силы с единицами энергии не является случайным. Работа по вращению системы, совершенная моментом M, рассчитывается по формуле:

Откуда получаем, что M также может быть выражен в джоулях на радиан (Дж/рад).

Потребляемая мощность электродвигателя

Ток ротора индуцируется через источник питания, к которому подсоединён электродвигатель, а магнитное поле частично создаётся напряжением. Входную мощность можно вычислить, если нам известны данные источника питания электродвигателя, т.е. напряжение, коэффициент мощности, потребляемый ток и КПД.

В Европе мощность на валу обычно измеряется в киловаттах. В США мощность на валу измеряется в лошадиных силах (л.с.).

Если вам необходимо перевести лошадиные силы в киловатты, просто умножьте соответствующую величину (в лошадиных силах) на 0,746. Например, 20 л.с. равняется (20 • 0,746) = 14,92 кВт.

И наоборот, киловатты можно перевести в лошадиные силы умножением величины в киловаттах на 1,341. Это значит, что 15 кВт равняется 20,11 л.с.

Соответствие электродвигателя нагрузке

Если нужно определить, отвечает ли вращающий момент определённого электродвигателя требованиям нагрузки, Вы можете сравнить характеристики скорости вращения/вращающего момента электродвигателя с характеристикой скорости вращения/ вращающего момента нагрузки. Вращающий момент, создаваемый электродвигателем, должен превышать потребный для нагрузки вращающий момент, включая периоды ускорения и полной скорости вращения.

Характеристика зависимости вращающего момента от скорости вращения стандартного электродвигателя и центробежного насоса.

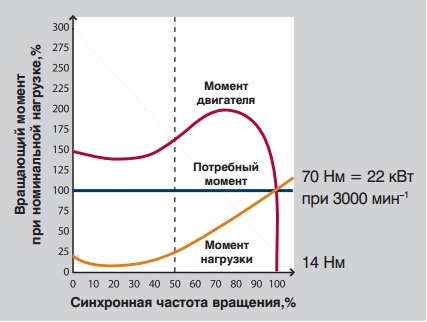
Если мы посмотрим на характеристику , то увидим, что при ускорении электродвигателя его пуск производится при токе, соответствующем 550% тока полной нагрузки.

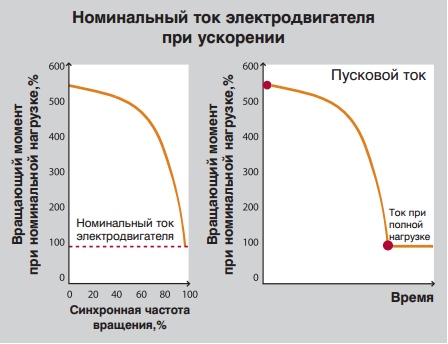
Когда двигатель приближается к своему номинальному значению скорости вращения, ток снижается. Как и следовало ожидать, во время начального периода пуска потери на электродвигателе высоки, поэтому этот период не должен быть продолжительным, чтобы не допустить перегрева.

Очень важно, чтобы максимальная скорость вращения достигалась как можно точнее. Это связано с потребляемой мощностью: например, увеличение скорости вращения на 1% по сравнению со стандартным максимумом приводит к 3%-ному увеличению потребляемой мощности

Потребляемая мощность пропорциональна диаметру рабочего колеса насоса в четвертой степени.

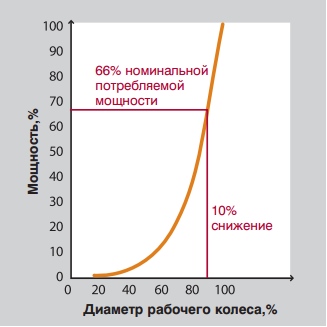
Уменьшение диаметра рабочего колеса насоса на 10% приводит к уменьшению потребляемой мощности на (1- (0.9 * 0.9 * 0.9 * 0.9)) * 100 = 34%, что равно 66% номинальной мощности. Эта зависимость определяется исключительно на практике, так как зависит от типа насоса, конструкции рабочего колеса и от того, насколько вы уменьшаете диаметр рабочего колеса.

Расчет крутящего момента – формула

Примечание: при расчете стоит учесть коэффициент проскальзывания асинхронного двигателя. Номинальное количество оборотов двигателя не совпадает с реальным. Точное количество оборотов вы сможете найти, зная маркировку, в таблице выше.

Расчет онлайн

Для расчета крутящего момента электродвигателя онлайн введите значение мощности ЭД и реальную угловую скорость (количество оборотов в минуту)

тут будет калькулятор

После расчета крутящего момента, посмотрите схемы подключения асинхронных электродвигателей звездой и треугольником на сайте «Слобожанского завода»

Харьков, Полтавский шлях, 56, тел.: +38

2021 Слобожанский электромеханический завод. Все права защищены

https://youtube.com/watch?v=NVd8prEdHF8

Расчет вала

Условие задачи:

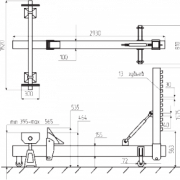
К стальному валу, состоящему из 4-х участков длиной l1…l4 приложено четыре сосредоточенных момента М1…М4 (см. рис. 1 ).

Требуется:

Построить эпюру крутящих моментов Мкр, подобрать диаметр вала из расчета на прочность, построить эпюру максимальных касательных напряжений τmax, построить эпюру углов закручивания φ вала и определить наибольший относительный угол закручивания вала.

Нагрузки, кН×м:

• М1 = -4,5;
• М2 = -2,6;
• М3 = -3,1;
• М4 = -2,0;

Длина участков, м:

• l1 = 0,9;
• l2 = 0,6;
• l3 = 0,9;
• l4 = 0,4;

Указания:

Вычертить схему вала в соответствии с исходными данными. Знаки моментов в исходных данных означают: плюс – момент действует против часовой стрелки относительно оси Z, минус – по часовой стрелке (см. навстречу оси Z). В дальнейшем значения моментов принимать по абсолютной величине. Участки нумеровать от опоры. Допускаемое касательное напряжение для стали принимать равным 100 МПа.

Решение:

1. Определим методом сечений значения крутящих моментов на каждом силовом участке от свободного конца вала. Крутящий момент равен алгебраической сумме внешних моментов, действующих на вал по одну сторону сечения.

• МIV = -М1 = -4,5 (кН×м);
• МIII = -М1 — М2 = -4,5 — 2,6 = -7,1 (кН×м);
• МII = -М1 — М2 – М3 = -4,5 – 2,6 – 3,1 = -10,2 (кН×м);
• МI = -М1 — М2 – М3 – М4 = -4,5 – 2,6 – 3,1 – 2,0 = -12,2 (кН×м).

2. Подберем сечение вала из расчета на прочность при кручении по полярному моменту сопротивления для участка, где величина крутящего момента максимальная (без учета знака):

WP≥ Мкр/ .

Так как для круглого сечения полярный момент равен: Wр = πD3/16, то можно записать:

D ≥ 3√(16Мкр/π) ≥ 3√(16×12,2×103/3,14×) = 0,0855 м или D ≥ 85,5 мм.(Здесь и далее знак «√» означает квадратный корень из выражения)

В соответствии со стандартным рядом, предусмотренным ГОСТ 12080-66, принимаем диаметр вала D = 90 мм.

3. Определим угол закручивания для каждого участка вала по формуле:

φ = Мкр×l/G×Iр,

где G – модуль упругости 2-го рода; для стали G = 8×1010 Па;Ip – полярный момент инерции (для круглого сечения Iр = πD4/32 ≈ 0,1D4, м4). Произведение G×Iр = 8×1010×0,1×0,094 ≈ 524880 Н×м2 – жесткость сечения данного вала при кручении.

Расчитываем углы закручивания на каждом участке:

• φI = -12,2×103×0,9/524880 = -0,0209 рад;
• φII = -10,2×103×0,6/524880 = -0,0116 рад;
• φIII = -7,1×103×0,9/524880 = -0,0122 рад;
• φIV = -4,5×103×0,4/524880 = -0,0034 рад.

4. Определяем углы закручивания сечений вала, начиная от жесткой заделки (опоры):

• φ0-0 = 0 рад;
• φ1-1 = φI= -0,0209 рад;
• φ2-2 = φI + φII= -0,0209 — 0,0116 = -0,0325 рад;
• φ3-3 = φI + φII + φIII= -0,0209 — 0,0116 — 0,0122 = -0,0447 рад;
• φ4-4 = φI + φII + φIII + φIV = -0,0209 — 0,0116 — 0,0122 -0,0034 = -0,0481 рад.

5. Определяем максимальное касательное напряжение на каждом силовом участке по формуле:

τmax = Мкр/Wp = 16Мкр/πD3≈ 5Мкр/D3.

Тогда:

• τmaxIV = 5×-4,5×103/0,093 = -30864197 Па ≈ -30,086 МПа;
• τmaxIII = 5×-7,1×103/0,093 = -48696844 Па ≈ -48,700 МПа;
• τmaxII = 5×-10,2×103/0,093 = -69958847 Па ≈ -69,959 МПа;
• τmaxI = 5×-12,2×103/0,093 = -83676268 Па ≈ -83,676 МПа.

6. Наибольший относительный угол закручивания Θmax определим по формуле:

Θmax = МКРmax/G×Iр = -12,2×103/524880 = 0,0232 рад/м.

7. По результатам расчетов строим эпюры крутящих моментов Мкр, касательных напряжений τmax и углов закручивания φ (см. рис. 2).

***

Учебные дисциплины

• Инженерная графика
• МДК.01.01. «Устройство автомобилей»
• Общее устройство автомобиля
• Автомобильный двигатель
• Трансмиссия автомобиля
• Рулевое управление
• Тормозная система
• Подвеска
• Колеса
• Кузов
• Электрооборудование автомобиля
• Основы теории автомобиля
• Основы технической диагностики
• Основы гидравлики и теплотехники
• Метрология и стандартизация
• Сельскохозяйственные машины
• Основы агрономии
• Перевозка опасных грузов
• Материаловедение
• Менеджмент
• Техническая механика
• Советы дипломнику

Олимпиады и тесты

• «Инженерная графика»
• «Техническая механика»
• «Двигатель и его системы»
• «Шасси автомобиля»
• «Электрооборудование автомобиля»

Время пуска электрдвигателя

Если нам необходимо подобрать типоразмер электродвигателя для определённой нагрузки, например для центробежных насосов, основная наша задача состоит в том, чтобы обеспечить соответствующий вращающий момент и мощность в номинальной рабочей точке, потому что пусковой момент для центробежных насосов довольно низкий. Время пуска достаточно ограниченно, так как вращающий момент довольно высокий.

Нередко для сложных систем защиты и контроля электродвигателей требуется некоторое время для их пуска, чтобы они могли замерить пусковой ток электродвигателя. Время пуска электродвигателя и насоса рассчитывается с помощью следующей формулы:

tпуск = время, необходимое электродвигателю насоса, чтобы достичь частоты вращения при полной нагрузке

n = частота вращения электродвигателя при полной нагрузке

Iобщ = инерция, которая требует ускорения, т.е. инерция вала электродвигателя, ротора, вала насоса и рабочих колёс.

Момент инерции для насосов и электродвигателей можно найти в соответствующих технических данных.

Мизб = избыточный момент, ускоряющий вращение. Избыточный момент равен вращающему моменту электродвигателя минус вращающий момент насоса при различных частотах вращения.

Мизб можно рассчитать по следующим формулам:

Как видно из приведённых вычислений, выполненных для данного примера с электродвигателем мощностью 4 кВт насоса CR, время пуска составляет 0,11 секунды.

Процесс вращения

Прежде чем рассматривать концепцию вращающего момента, дадим характеристику систем, к которым может быть применена эта концепция. Система вращения предполагает наличие в ней оси, вокруг которой осуществляется круговое движение или поворот. Расстояние от этой оси до материальных точек системы называется радиусом вращения.

С точки зрения кинематики, процесс характеризуется тремя угловыми величинами:

• углом поворота θ (измеряется в радианах);
• угловой скоростью ω (измеряется в радианах в секунду);
• ускорением угловым α (измеряется в радианах в секунду квадратную).

Эти величины связаны друг с другом следующими равенствами:

Примерами вращения в природе являются движения планет по своим орбитам и вокруг своих осей, движения смерчей. В быту и технике рассматриваемое движение характерно для моторов двигателей, гаечных ключей, строительных кранов, открывания дверей и так далее.

Момент силы относительно оси

Предположим, что данные являются точкой O (полюс) и мощность P. В точке O мы принимаем начало прямоугольной системы координат. Момент силы Р по отношению к полюсным O представляет собой вектор М из (Р), (рисунок ниже).

Любая точка A на линии P имеет координаты (xo , yo , zo ). Вектор силы P имеет координаты Px , Py, Pz. Комбинируя точку A (xo, yo, zo ) с началом системы, мы получаем вектор p. Координаты вектора силы P относительно полюса O обозначены символами Mx, My, Mz. Эти координаты могут быть вычислены как минимумы данного определителя, где ( i, j, k) — единичные векторы на осях координат (варианты): i, j, k

После решения определителя координаты момента будут равны:

Координаты вектора моментов Mo (P) называются моментами силы относительно соответствующей оси. Например, момент силы P относительно оси Oz окружает шаблон:

Mz = Pyxo — Pxyo

Этот паттерн интерпретируется геометрически так, как показано на рисунке ниже.

Если сила лежит в плоскости Oxy, то zo = 0 и Pz = 0 (см. Рисунок ниже).

Момент силы P по отношению к точке (полюсу) O составляет: Mx = 0, My = 0, Mo (P) = Mz = Pyxo — Pxyo.

Метка крутящего момента: плюс (+) — вращение силы вокруг оси O по часовой стрелке, минус (-) — вращение силы вокруг оси O против часовой стрелки.

Тимеркаев Борис — 68-летний доктор физико-математических наук, профессор из России. Он является заведующим кафедрой общей физики в Казанском национальном исследовательском техническом университете имени А. Н. ТУПОЛЕВА — КАИ

Пусковые режимы электрических моторов

Существуют и применяются на практике разные пусковые режимы асинхронных электродвигателей. Каждый имеет свои плюсы и минусы в зависимости от технических характеристик моторов и нагрузки.

Выбор конкретного режима пуска определяется электрическими, механическими, экономическими факторами. Вид управляемой нагрузки, также является важным фактором выбора режима запуска. Рассмотрим наиболее часто практикуемые варианты пусков.

Пусковые режимы свободно вращающегося мотора

Этот режим пуска асинхронного электродвигателя видится самым простым из всех существующих схем. Здесь статор мотора напрямую подключается к источнику питания. Электродвигатель стартует в соответствии с определённой для него характеристикой.

Момент электродвигателя

Мощность связывает вращающий момент с частотой вращения, чтобы определить общий объём работы, который должен быть выполнен за определённый промежуток времени.

Рассмотрим взаимодействие между вращающим моментом, мощностью и частотой вращения, а также их связь с электрическим напряжением на примере электродвигателей Grundfos. Электродвигатели имеют одну и ту же номинальную мощность как при 50 Гц, так и при 60 Гц.

Это влечёт за собой резкое снижение вращающего момента при 60 Гц: частота 60 Гц вызывает 20%-ное увеличение числа оборотов, что приводит к 20%-ному уменьшению вращающего момента. Большинство производителей предпочитают указывать мощность электродвигателя при 60 Гц, таким образом, при снижении частоты тока в сети до 50 Гц электродвигатели будут обеспечивать меньшую мощность на валу и вращающий момент. Электродвигатели обеспечивают одинаковую мощность при 50 и 60 Гц.

Графическое представление вращающего момента электродвигателя изображено на рисунке.

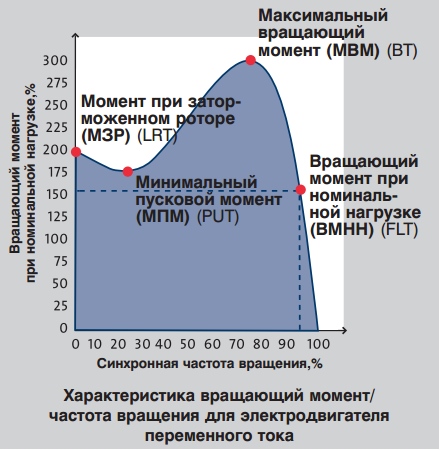
Иллюстрация представляет типичную характеристику вращающий момент/частота вращения. Ниже приведены термины, используемые для характеристики вращающего момента электродвигателя переменного тока.

Пусковой момент (Мп): Механический вращающий момент, развиваемый электродвигателем на валу при пуске, т.е. когда через электродвигатель пропускается ток при полном напряжении, при этом вал застопорен.

Минимальный пусковой момент (Ммин): Этот термин используется для обозначения самой низкой точки на кривой вращающий момент/частота вращения электродвигателя, нагрузка которого увеличивается до полной скорости вращения. Для большинства электродвигателей Grundfos величина минимального пускового момента отдельно не указывается, так как самая низкая точка находится в точке заторможенного ротора. В результате для большинства электродвигателей Grundfos минимальный пусковой момент такой же, как пусковой момент.

Блокировочный момент (Мблок): Максимальный вращающий момент — момент, который создаёт электродвигатель переменного тока с номинальным напряжением, подаваемым при номинальной частоте, без резких скачков скорости вращения. Его называют предельным перегрузочным моментом или максимальным вращающим моментом.

Вращающий момент при полной нагрузке (Мп.н.): Вращающий момент, необходимый для создания номинальной мощности при полной нагрузке.

Факторы, влияющие на величину крутящих моментов

Из примера с лошадью легко догадаться, что в данном случае значение КМ будет во многом определяться мышечной массой животного. Применительно к автомобильному двигателю внутреннего сгорания эта величина зависит от рабочего объема силовой установки, а также от:

• уровня рабочего давления внутри цилиндров;
• размера поршня;
• диаметра кривошипа коленвала.

Прямая зависимость наблюдается также между КМ и радиусом кривошипа коленвала. Однако конструкция современных автомобильных двигателей такова, что не позволяет варьировать значения момента в широких пределах, из-за чего возможности добиться повышенного крутящего момента за счет радиуса кривошипа коленчатого вала у конструкторов ДВС невелики. Вместо этого разработчики прибегают к таким способам увеличить момент, как использование технологий турбонаддува, увеличение степени сжатия, оптимизация процесса сгорания топлива, использование впускных коллекторов специальных конструкций, и т.д.

Важно, что КМ увеличивается с ростом оборотов двигателя, однако после достижения максимума на определенном диапазоне крутящий момент понижается несмотря на продолжающийся прирост частоты вращения коленвала

Общие сведения

Кода на тело действует сила в определенном направлении — тело поворачивается. Это стремление силы поворачивать тело описывается физической величиной — вращающим моментом или моментом силы. Сама сила, которая вызывает поворот или кручение, а также расстояние между точкой ее приложения и точкой вращения тела влияют на момент силы

В данном случае сила — векторная величина, поэтому важно также и направление силы, то есть угол между направлением силы и отрезком, соединяющим точку приложения силы и центр вращения тела. Если этот угол прямой, то есть сила приложена перпендикулярно отрезку, то момент силы — максимальный

По мере того, как сила становится параллельной отрезку, момент силы уменьшается. То есть, чем ближе угол к 0° или 180°, тем слабее момент силы, пока он не становится равным нулю, когда направление силы параллельно отрезку. Удобно представить момент силы, как комбинацию расстояния, на которое удалена сила от точки вращения, и силы, которая необходима, чтобы заставить тело вращаться с определенной интенсивностью.

Момент силы имеет наибольшую величину, если сила, действующая на тело, перпендикулярна отрезку, соединяющему точку вращения и точку приложения силы. На рисунке силы F2, F3, и F5 создают наибольший момент силы.

Давайте посмотрим на эту взаимосвязь на иллюстрации. Здесь силы F2, F3 и F5 перпендикулярны отрезку между осью вращения, обозначенной голубым цветом в центре штурвала, и точкой приложения силы. Создаваемый ими момент силы — максимален. С другой стороны, силы F1 и F4 приложены под углом, отличным от 90°, и создаваемый ими момент силы не максимален. То есть, момент силы этих двух сил отличается от момента силы других трех сил, хотя величина всех сил на рисунке — одинакова.

Чтобы повернуть тело под воздействием силы с заданными условиями, необходимо создать момент силы. Так как эта величина зависит и от расстояния, и от силы, то для получения заданного момента можно изменять либо силу, либо расстояние от точки приложения до точки вращения. Люди используют эту зависимость испокон веков.

Правило моментов

Вернемся к нашим баранам качелям. Мы умудряемся на них качаться, потому что существует вращательное действие — момент. Силы, с которыми мы действуем на разные стороны этих качелей могут быть разными, но вот моменты должны быть одинаковыми.

Правило моментов говорит о том, что если рычаг не вращается, то сумма моментов сил, поворачивающих рычаг против часовой стрелки, равна сумме моментов сил, поворачивающих рычаг по часовой стрелке.

Это условие выполняется относительно любой точки.

Правило моментов M1 + M2 +…+ Mn = M’1 + M’2 +…+ M’n M1 + M2 +…+ Mn — сумма моментов сил, поворачивающих рычаг по часовой стрелке

Давайте рассмотрим этот закон на примере задач.

Задача 1

К левому концу невесомого стержня прикреплен груз массой 3 кг.

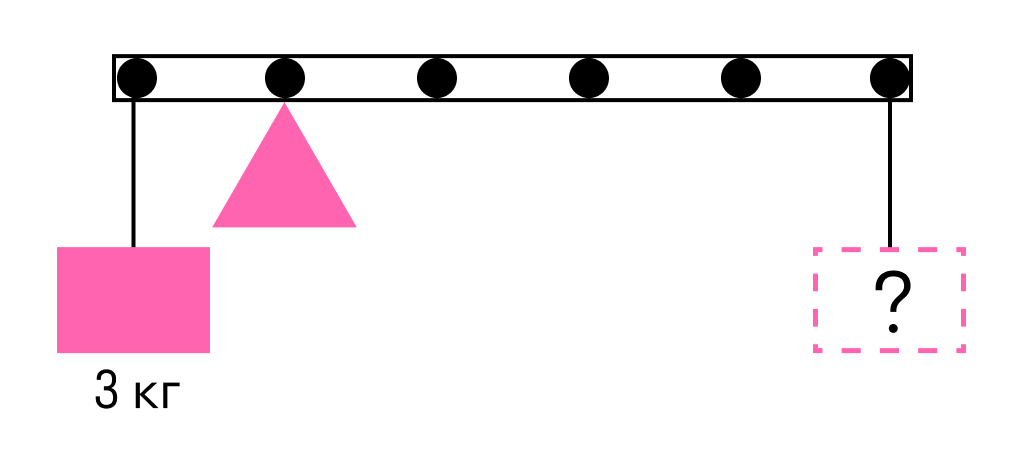
Стержень расположили на опоре, отстоящей от его левого конца на 0,2 длины стержня. Чему равна масса груза, который надо подвесить к правому концу стержня, чтобы он находился в равновесии?

Решение:

Одним из условий равновесия стержня является то, что полный момент всех внешних сил относительно любой точки равен нулю. Рассмотрим моменты сил относительно точки опоры. Момент, создаваемый левым грузом равен mgL5 он вращает стержень против часовой стрелки. Момент, создаваемый правым грузом:Mg4L5 — он вращает по часовой.

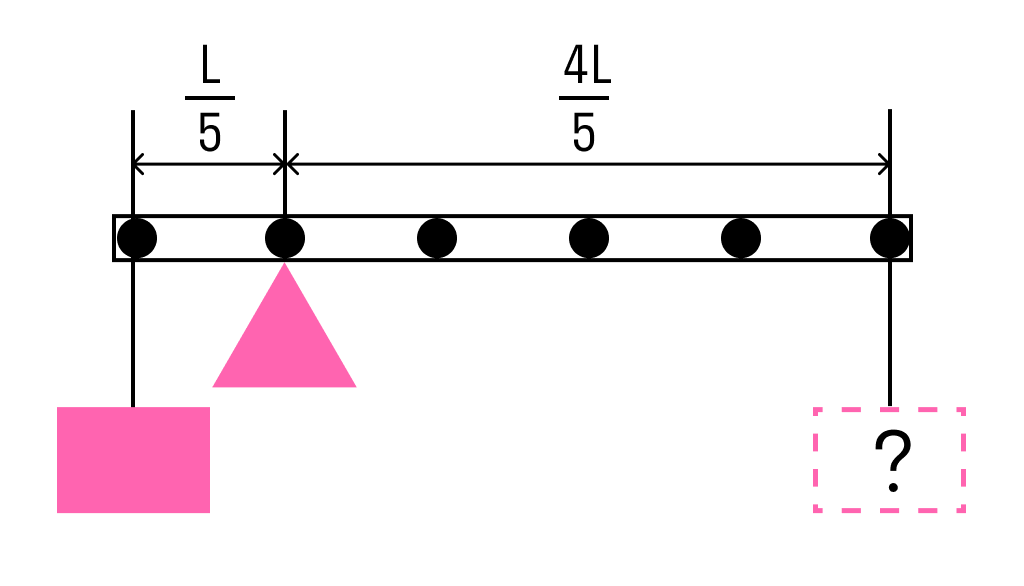
Приравнивая моменты, получаем, что для равновесия к правому концу стержня необходимо подвесить груз массой
M = m : 4 = 3 : 4 = 0,75 кг

Ответ: для равновесия к правому концу стержня необходимо подвесить груз массой 0,75 кг

Задача 2

Путешественник несёт мешок с вещами на лёгкой палке. Чтобы удержать в равновесии груз весом 80 Н, он прикладывает к концу B палки вертикальную силу 30 Н. OB = 80 см. Чему равно OA?

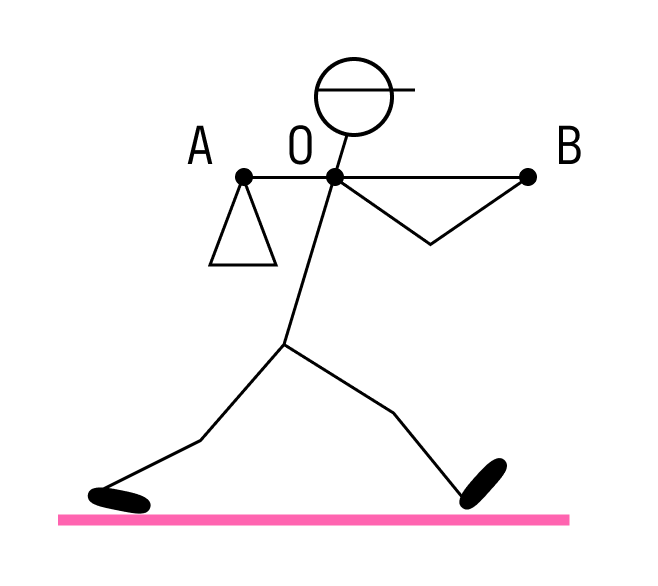
Решение:

По правилу рычага: FB/FA=|OA|/|OB| где FA и FB — силы, приложенные соответственно к точкам A и B. Выразим длину OA:

|OA|=FB/FA)*|OB|=30/80*80=30 см

Ответ: расстояние ОА равно 30 см

Задача 3

Тело массой 0,2 кг подвешено к правому плечу невесомого рычага (см. рисунок). Груз какой массы надо подвесить ко второму делению левого плеча рычага для достижения равновесия?

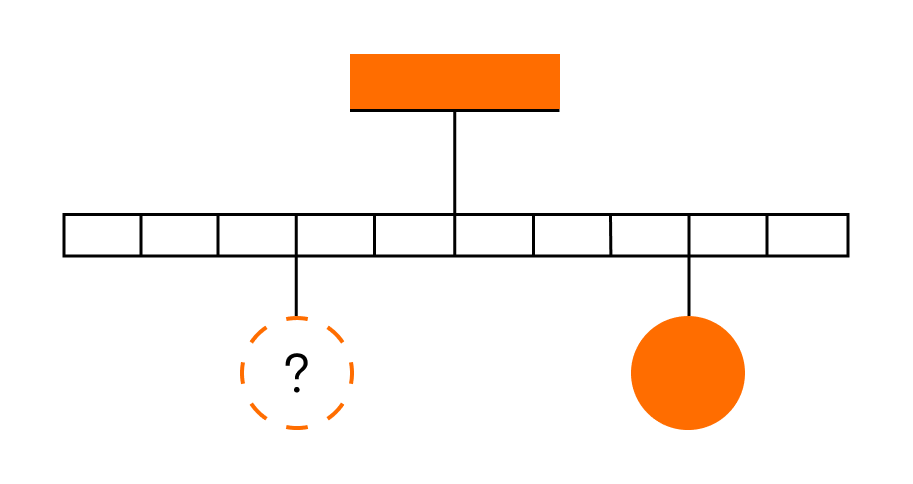
Решение:

По правилу рычага m1g*l1=m2g*l2

Отсюда m2=l1/l2*m1=3/2*0,2 = 0,3 кг

Ответ: Масса груза равна 0,3 кг

Задача 4

На железной дороге для натяжения проводов используется показанная на рисунке система, состоящая из легких блоков и тросов, натягиваемых тяжелым грузом. Чему равна сила натяжения провода?

Решение:

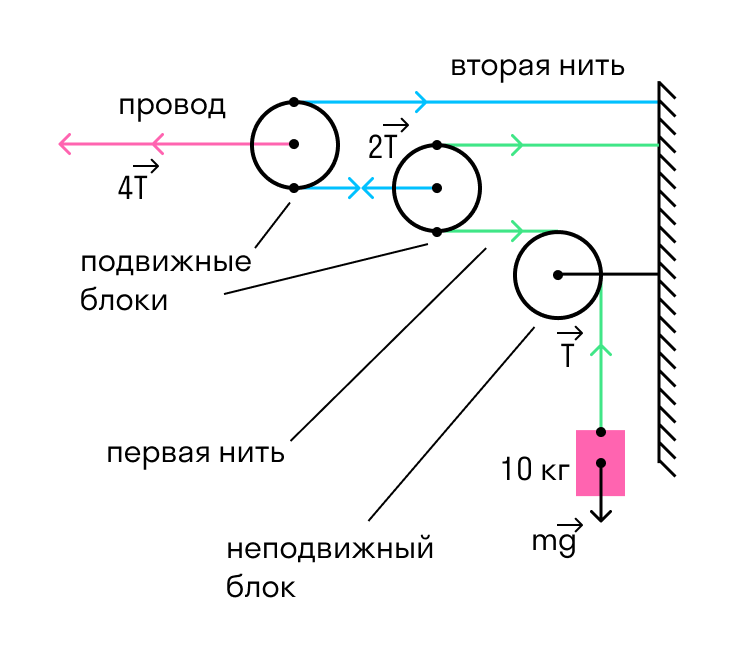
Система на рисунке состоит из трех блоков: двух подвижных и одного неподвижного. Назначение неподвижного блока заключается только в том, что он меняет направление действия силы, однако никакого выигрыша в силе при этом не возникает. Каждый подвижный блок, напротив, дает выигрыш в силе.

Определим силу, с которой натянута первая нить. Груз растягивает ее с силой:
T = mg = 10*10 = 100 Н

Рассмотрим теперь первый подвижный блок. Так как вся система статична, полная сила, действующая на этот блок, должна быть равна нулю. Первая нить тянет его направо с суммарной силой 2T, значит, натяжение второй нити тоже должно быть равно 2T (вот он — выигрыш в силе). Аналогичное рассмотрение для второго подвижного блока показывает, что натяжение провода должно быть равно

4T = 4*100= 400 Н

Ответ: натяжение провода равно 400 Н

Задача 5 — a.k.a самая сложная задачка

Под действием силы тяжести mg груза и силы F рычаг, представленный на рисунке, находится в равновесии. Вектор силы F перпендикулярен рычагу, груз на плоскость не давит. Расстояния между точками приложения сил и точкой опоры, а также проекции этих расстояний на вертикальную и горизонтальную оси указаны на рисунке.

Если модуль силы F равен 120 Н, то каков модуль силы тяжести, действующей на груз?

Решение:

Одним из условий равновесия рычага является то, что полный момент всех внешних сил относительно любой точки равен нулю. Рассмотрим моменты сил относительно опоры рычага. Момент, создаваемый силой F, равен F*5 м и он вращает рычаг по часовой стрелке. Момент, создаваемый грузом относительно этой точки — mg*0,8 м, он вращает против часовой. Приравнивая моменты, получаем выражение для модуля силы тяжести

mg=F*5/0,8=120*5/0,8=750Н

Ответ: модуль силы тяжести, действующей на груз равен 750 Н

Когда момент силы обращается в ноль

Рассмотрим внимательнее формулу для момента силы.

\

В правой части формулы находятся три множителя: \( F \) , \(d\) и  \( sin(\gamma) \)

Если любой из трех множителей будет равен нулю, то правая часть уравнения обратится в ноль.

Левая часть уравнения, при этом, также, обратится в ноль. Потому, что между левой и правой частями записан знак равенства.

Кратко: Вращательный момент будет нулевым в любом из таких случаев:

1. \( F = 0\) – когда вращающая сила отсутствует;
2. \(d = 0 \) – когда сила приложена к точке вращения;
3. \( sin(\gamma) = 0 \) – когда сила \( F \) и величина \(d \) лежат на одной прямой. В таком случает, угол между величинами \( F \) и \(d \) равен нулю;

Действительно: \( sin(0) = 0 \), такое будет, когда \( F || d \)

Эти три случая изображены на рисунке 6.

Рис. 6. Сверху вниз представлены три случая, в которых вращательный момент обращается в ноль

На рисунке 6: черная стрелка – это вектор силы, красная линия – это расстояние между точкой приложения силы и точкой вращения.

Сверху вниз представлены три случая для нулевого вращательного момента.

• В верхней части рисунка сила отсутствует;
• Средняя часть рисунка соответствует случаю, когда сила (черная стрелка) приложена к точке, вокруг которой тело может вращаться;
• Внизу — сила \( F \) параллельна величине \(d \) — расстоянию между точкой приложения силы и точкой вращения.

Пусковые режимы асинхронных электродвигателей

Момент начала питания электродвигателя напряжением сети сопровождается высоким пусковым током. Поэтому, если участок линии электропередачи относительно слаб, фиксируется снижение напряжения, что оказывает влияние на работу рецептора. Падение напряжения может достигать значительных величин, что также сказывается на функциональности систем освещения. Исключить подобные явления призваны отраслевые правила, которыми запрещается пуск электродвигателей в режиме непосредственного старта, если оборудование выходит за пределы заданной мощности. Следует применять такие пусковые режимы электродвигателей, при которых питающая сеть и периферийное оборудование не испытывают дестабилизации в работе.

Типы опор и нагрузок

Фиксированная поддержка: Он может предложить три реакции в плоскости элемента (1 горизонтальная реакция, 1 вертикальная реакция, 1 моментная реакция).

Поддержка контактов: Он может предложить две реакции в плоскости элемента (1 горизонтальная реакция, 1 вертикальная реакция).

Роликовая опора: Он может предложить только одну реакцию в плоскости члена (1 вертикальная реакция).

Концентрированная или точечная нагрузка: При этом вся интенсивность нагрузки ограничена конечной площадью или точкой.

Равномерно распределенная нагрузка :  При этом вся интенсивность нагрузки постоянна по длине балки.

Равномерно изменяющаяся нагрузка :  При этом вся интенсивность нагрузки изменяется линейно по длине балки.

Типы опор и нагрузок