Формула средней скорости

Средняя скорость

Факт изменения скорости тела при неравномерном движении не всегда необходимо учитывать, при рассмотрении движении тела на большом участке пути в целом (нам не важна скорость в каждый момент времени) удобно ввести понятие средней скорости.

Например, делегация школьников добирается из Новосибирска в Сочи поездом. Расстояние между этими городами по железной дороге составляет приблизительно 3300 км. Скорость поезда, когда он только выехал из Новосибирска составляла

Рис. 6. Иллюстрация к примеру

Когда рассматривается движение тела на большом участке пути в целом, удобнее ввести понятие средней скорости.

Средней скоростью называют отношение полного перемещения, которое совершило тело, ко времени, за которое совершено это перемещение (рис. 7).

Рис. 7. Средняя скорость

Данное определение не всегда является удобным. Например, спортсмен пробегает 400 м – ровно один круг. Перемещение спортсмена равно 0 (рис. 8), однако мы понимаем, что его средняя скорость нулю равна быть не может.

Рис. 8. Перемещение равно 0

На практике чаще всего используется понятие средней путевой скорости.

Средняя путевая скорость – это отношение полного пути, пройденного телом, ко времени, за которое путь пройден (рис. 9).

Рис. 9. Средняя путевая скорость

Существует еще одно определение средней скорости.

Средняя скорость – это та скорость, с которой должно двигаться тело равномерно, чтобы пройти данное расстояние за то же время, за которое оно его прошло, двигаясь неравномерно.

Из курса математики нам известно, что такое среднее арифметическое. Для чисел 10 и 36 оно будет равно:

Для того чтобы узнать возможность использования этой формулы для нахождения средней скорости, решим следующую задачу.

Велосипедист поднимается со скоростью 10 км/ч на склон, затрачивая на это 0,5 часа. Далее со скоростью 36 км/ч спускается вниз за 10 минут. Найдите среднюю скорость велосипедиста (рис. 10).

Рис. 10. Иллюстрация к задаче

Дано:Найти:

Так как единица измерения данных скоростей – км/ч, то и среднюю скорость найдем в км/ч. Следовательно, данные задачи не будем переводить в СИ. Переведем

Средняя скорость равна:

Полный путь (

Путь подъема на склон равен:

Путь спуска со склона равен:

Время, за которое пройден полный путь, равно:

Ответ:

Исходя из ответа задачи, видим, что применять формулу среднего арифметического для вычисления средней скорости нельзя.

Не всегда понятие средней скорости полезно для решения главной задачи механики. Возвращаясь к задаче про поезд, нельзя утверждать, что если средняя скорость на всем пути поезда равна Мгновенная скорость

Среднюю скорость, измеренную за бесконечно малый промежуток времени, называют мгновенной скоростью тела (для примера: спидометр автомобиля (рис. 11) показывает мгновенную скорость).

Рис. 11. Спидометр автомобиля показывает мгновенную скорость

Существует еще одно определение мгновенной скорости.

Мгновенная скорость – скорость движения тела в данный момент времени, скорость тела в данной точке траектории (рис. 12).

Рис. 12. Мгновенная скорость

Для того чтобы лучше понять данное определение, рассмотрим пример.

Пусть автомобиль движется прямолинейно по участку шоссе. У нас есть график зависимости проекции перемещения от времени для данного движения (рис. 13), проанализируем данный график.

Рис. 13. График зависимости проекции перемещения от времени

На графике видно, что скорость автомобиля не постоянная. Допустим, необходимо найти мгновенную скорость автомобиля через 30 секунд после начала наблюдения (в точке A). Пользуясь определением мгновенной скорости, найдем модуль средней скорости за промежуток времени от

Рис. 14. График зависимости проекции перемещения от времени

Рассчитываем среднюю скорость на данном участке времени:

Для того чтобы проверить правильность нахождения мгновенной скорости, найдем модуль средней скорости за промежуток времени от

Рис. 15. График зависимости проекции перемещения от времени

Рассчитываем среднюю скорость на данном участке времени:

Получили два значения мгновенной скорости автомобиля через 30 секунд после начала наблюдения. Точнее будет то значение, где интервал времени меньше, то есть

A

Мгновенная скорость – это векторная величина. Поэтому, кроме ее нахождения (нахождения ее модуля), необходимо знать, как она направлена.

Направление мгновенной скорости совпадает с направлением перемещения тела.

Если тело движется криволинейно, то мгновенная скорость направлена по касательной к траектории в данной точке (рис. 16).

Рис. 16. Направление мгновенной скорости

Задачи на движение с переменной скоростью

Усложним задачу. Пусть у нас будет всадник, который первые t1 = 15 мин. скакал на лошади со скоростью v1 = 20 км/час, вторые полчаса t2 = 0,5 час. лошадь шла шагом со скоростью v2 = 6 км/час, а ещё t3 = 36 мин. бежала со скоростью v3 = 15 км/час. Как найти среднюю скорость (V ср) движения всадника и лошади?

Всадник был в пути t = t1 + t2 + t3

В нашем случае весь путь равен сумме трёх отрезков, которые вычисляются как произведение скорости на время, о чём написано в статье Как найти скорость, время расстояние:

• S = S1 + S2 + S3 = v1*t1 + v2*t2 + v3*t3
• V ср = S/t = (v1*t1 + v2*t2 + v3*t3) / (t1 + t2 + t3)

Чтобы не путаться с часами и минутами, переводим все минуты в часы: 15 мин. = 0,4 час, 36 мин. = 0,6 час. Подставляем числовые значения в последнюю формулу:

V ср = (20*0,4 + 0,5*6 + 0,6*15) / (0,4 + 0,5 + 0,6) = (8 + 3 + 9) / (0,4 + 0,5 + 0,6) = 20 / 1,5 = 13,3 км/час

Ответ: средняя скорость V ср = 13,3 км/час.

Движение по кольцевым трассам

      Задача 6. (www.reshuege.ru) Из пункта   A   круговой трассы длиной   46   км выехал велосипедист, а через   20   минут из пункта   A   следом за велосипедистом отправился мотоциклист. Через   5   минут после отправления мотоциклист догнал велосипедиста в первый раз, а еще через   46   минут после этого мотоциклист догнал велосипедиста во второй раз. Найдите скорости велосипедиста и мотоциклиста.

      Решение. К тому моменту, когда мотоциклист в первый раз догнал велосипедиста, мотоциклист ехал   5   минут, а велосипедист ехал   25   минут, причем проехали они один и тот же путь. Отсюда вытекает, что скорость мотоциклиста в   5   раз больше скорости велосипедиста.

      Таким образом, обозначив буквой   v   (км/час) скорость велосипедиста, получаем, что скорость мотоциклиста равна   5v   (км/час).

      В условии задачи дано время, прошедшее между двумя последовательными встречами мотоциклиста и велосипедиста, –   46   минут. Это время необходимо выразить в часах, чтобы все единицы измерения были согласованными:

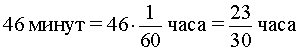
      Изобразим данные задачи, касающиеся движения мотоциклиста и велосипедиста между первой и второй встречами, на рисунке 6.

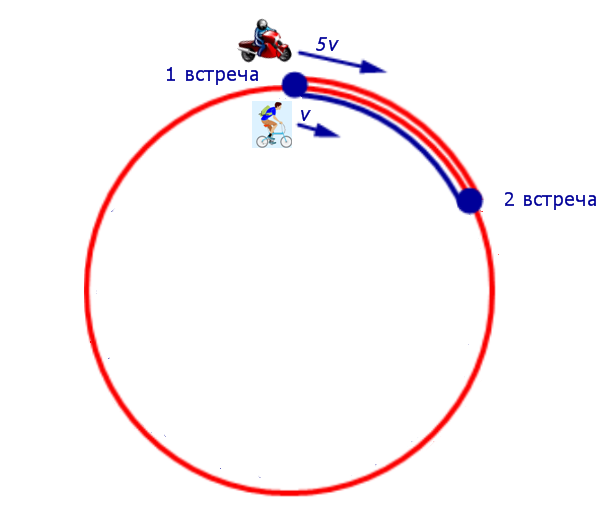
Рис. 6

      Поскольку за время часа, прошедшее от момента первой встречи до момента второй встречи, мотоциклист проехал   46   км (вся круговая трасса) плюс путь, который проехал велосипедист за часа, то можно составить следующее уравнение:

      Решая это уравнение, находим скорость велосипедиста:

v = 15 .

      Ответ. Скорость велосипедиста   15   км/час, скорость мотоциклиста   75   км/час.

      Задача 7. На дороге, представляющей собой окружность длиной   60   км, пункты   A   и   B   являются диаметрально противоположными точками. Велосипедист выехал из пункта   A   и сделал два круга. Первый круг он прошел с постоянной скоростью, после чего уменьшил скорость на   5   км/час. Время между двумя прохождениями велосипедиста через пункт   B   равно   5   часам. Найти скорость, с которой велосипедист прошел первый круг.

      Решение. Для определенности будем считать, что велосипедист двигался по кругу по часовой стрелке и рассмотрим рисунок 7.

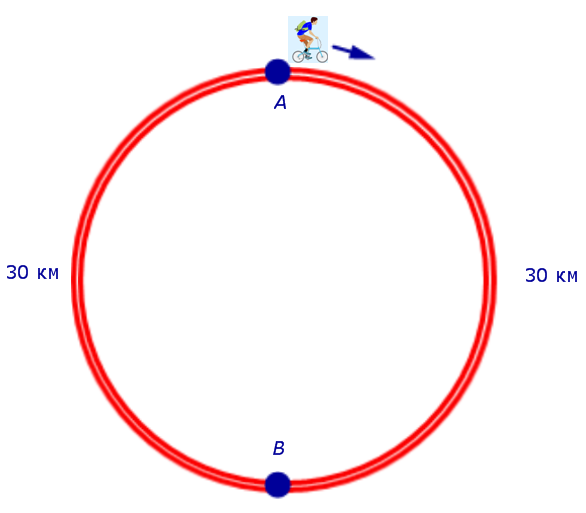
Рис. 7

      Если обозначить буквой   v   (км/час) скорость, с которой велосипедист прошел первый круг, то скорость велосипедиста на втором круге будет равна   v – 5   (км/час), и можно составить уравнение

      Решая это уравнение, находим скорость велосипедиста на первом круге:

      Поскольку скорость велосипедиста на первом круге больше, чем   5   км/час, то первый корень должен быть отброшен.

      Ответ.   15   км/час.

      Желающие ознакомиться с примерами решения различных задач по теме «Проценты» и применением процентов в экономике и финансовой математике могут посмотреть разделы нашего справочника «Проценты. Решение задач на проценты», «Простые и сложные проценты. Предоставление кредитов на основе процентной ставки», а также наши учебные пособия «Задачи на проценты» и «Финансовая математика».

      Приемы, используемые для решения задач на выполнение работ представлены в разделе нашего справочника «Задачи на выполнение работ».

      С примерами решения задач на смеси, сплавы и растворы можно ознакомиться в разделе нашего справочника «Задачи на смеси, сплавы и растворы».

Сколько шагов в километре

Перед тем как начать активно ходить и преодолевать расстояния в 10 000 шагов, следует изучить технику движения и узнать, сколько шагов в километре именно в вашем случае. Современному человеку нет необходимости внимательно считать шаги при ходьбе, преодолевая всю дистанцию. Для этого задания используются специальные гаджеты, приложения для смартфонов и среднестатистические данные.

Средние показатели

Длина шага даже для одного человека – величина непостоянная и зависит от таких факторов:

• рост, пол и вес человека;
• скорость передвижения;
• обувь;
• состояние здоровья;
• уровень физической подготовки;
• поверхность, по которой движется человек.

Статистические данные позволяют пользоваться для вычислений примерными значениями:

• средний шаг человека ростом 175 см — 80 см;
• средняя длина женского шага — 70 см.

Существует несколько способов рассчитать длину шага:

1. Замер длины: шагнуть в обычном темпе, измерить расстояние от кончиков пальцев ноги, оставшейся сзади, до кончиков пальцев ноги, поставленной впереди.
2. Вычисление средней длины: отмерить расстояние в 10 метров, посчитать количество шагов, разделить первую величину на вторую.
3. Использование специальной формулы, по которой длина шага зависит от роста человека.

Измерение расстояния в шагах

Проще всего определить расстояние высоким людям, длина шага которых при ходьбе в темпе выше среднего будет 1 м: 1000 шагов — 1 км. Остальным ходокам без применения специальных приспособлений рекомендуют воспользоваться табличными данными:

Расстояние в шагах для мужчин и женщин

Мужчины	Женщины
Длина 1 шага	0,8 м	0,7 м
Сколько шагов в 100 метрах	125	143
Сколько шагов в 1 км	1250	1430

Таким образом, сделав 5 000 шагов, человек пройдет от 3,5 до 4 км в зависимости от величины шага. Соответственно, 8 000 шагов это 5,5-6,5 км, а 10 000 шагов — около 8 км.

Измерение расстояния по времени

В среднем 1 км человек преодолевает в быстром темпе за 10 минут, эта величина будет другой при низкой скорости и небольшой длине шага. По времени 7 км пешком займет 1 час 10 минут. Рекомендованные японскими медиками 10 000 шагов (8 км) можно пройти за 1 час 20 минут с высокой скоростью.

Как рассчитать

Новичку цель в 10 000 шагов может показаться недосягаемой, а если перевести эту цифру в километры, расстояние становится нагляднее. Когда нет возможности использовать онлайн-калькулятор шагов, тренеры советуют один раз произвести перевод передвижения в километры и пользоваться индивидуальными данными.

Средняя длина шага женщины и мужчины рассчитывается по формуле: ДШ=(Р:4)+0,37, где

• ДШ — длина шага;
• Р — рост в метрах;
• 4 и 0,37 — коэффициенты.

При росте 170 см средняя величина составит (1,70/4)+0,37= 0,79 м.

Перевод шагов километры осуществляется путем несложных вычислений, рассмотрим на примере человека ростом 170 см с длиной шага 79 см:

• в 100 метрах — 100:0,79=126 шагов,
• в одном километре — 126*10=1 260 шагов;
• в 2 км — 2520 шагов;
• 5 км — 6 300.

Перевести 10 000 шагов в километры также просто двумя способами:

• 10 000:1260=7,9 км;
• 10 000*0,79=7900 м.

Не такая простая арифметика

Сводные данные показывают, что эталонные 10 000 шагов для людей разного роста, передвигающихся с разной скоростью, могут составлять от 6 до 8 км. Рассчитать длину ежедневного пешего прохождения, ориентируясь на показатели фитнес-гаджетов и приложений, тоже сложно, так как существует вероятность сбоя программы и неточного сбора данных. Например, некоторые шагомеры не учитывают ходьбу на месте, назад или в стороны.

Специалисты советуют произвести индивидуальный расчет длины шага в зависимости роста по формуле или с помощью онлайн-калькулятора, потом перевести в километры. Информация о том, сколько шагов составляют 100 метров, позволяет легко определить их количество в 1 км.

Сложение скоростей

Скорости движения тела в различных системах отсчёта связывает между собой классический
закон сложения скоростей.

Скорость тела относительно неподвижной системы отсчёта равна сумме
скоростей тела в подвижной системе отсчёта и самой подвижной системы
отсчёта относительно неподвижной.

Например, пассажирский поезд движется по железной дороге со скоростью 60 км/ч.
По вагону этого поезда идет человек со скоростью 5 км/ч. Если считать железную
дорогу неподвижной и принять её за систему отсчёта, то скорость человека относительно
системы отсчёта (то есть относительно железной дороги), будет равна сложению
скоростей поезда и человека, то есть

60 + 5 = 65, если человек идёт в том же направлении, что и поезд

60 – 5 = 55, если человек и поезд движутся в разных направлениях

Однако это справедливо только в том случае, если человек и поезд движутся по одной линии.
Если же человек будет двигаться под углом, то придётся учитывать этот угол, вспомнив о том,
что скорость – это векторная величина.

А теперь рассмотрим описанный выше пример более подробно – с деталями и картинками.

Итак, в нашем случае железная дорога – это неподвижная система отсчёта.
Поезд, который движется по этой дороге – это подвижная система отсчёта.
Вагон, по которому идёт человек, является частью поезда.

Скорость человека относительно вагона (относительно подвижной системы отсчёта) равна 5 км/ч.
Обозначим её буквой _Ч.

Скорость поезда (а значит и вагона) относительно неподвижной системы отсчёта
(то есть относительно железной дороги) равна 60 км/ч. Обозначим её буквой
_В. Иначе говоря, скорость
поезда – это скорость подвижной системы отсчёта относительно неподвижной системы отсчёта.

Скорость человека относительно железной дороги (относительно неподвижной системы отсчёта)
нам пока неизвестна. Обозначим её буквой .

Свяжем с неподвижной системой отсчёта (рис. 1.7) систему координат ХОY,
а с подвижной системой отсчёта – систему координат X_ПО_ПY_П
(см. также раздел ).
А теперь попробуем найти скорость человека относительно неподвижной системы отсчёта,
то есть относительно железной дороги.

За малый промежуток времени Δt происходят следующие события:

• Человек перемещается относительно вагона на расстояние _Ч
• Вагон перемещается относительно железной дороги на расстояние _B

= _Ч + _B

Это закон сложения перемещений. В нашем примере перемещение человека
относительно железной дороги равно сумме перемещений человека относительно вагона и
вагона относительно железной дороги.

Рис. 1.7. Закон сложения перемещений.

Закон сложения перемещений можно записать так:

_ЧB

Скорость человека относительно железной дороги равна:

 =  / Δt

= _Ч + _B

то

Скорость человека относительно вагона:

ΔЧ = Ч / Δt

ΔB = B / Δt

 = ΔЧ + ΔB

сложения скоростей
Скорость тела относительно неподвижной системы отсчёта равна сумме скоростей тела в подвижной системе отсчёта и скорости самой подвижной системы отсчёта относительно неподвижной.

Движение по окружности

Движение по окружности — простейший случай криволинейного движения тела, когда тело движется вокруг некоторой точки

Очень важно разделить движение по окружности и вращение тела

При вращательном движении тела все его точки описывают окружности, расположенные в параллельных плоскостях. Центры всех окружностей лежат при этом на одной прямой, перпендикулярной к плоскостям окружностей и называемой осью вращения. Ось вращения может располагаться внутри тела и за его пределами.

Движение тела по окружности с постоянной по модулю скоростью — это движение, при котором тело за любые равные промежутки времени описывает одинаковые дуги. Это очень похоже на равномерное движение, только в данном случае мы имеем дело с дугами.

При движении по окружности тело двигается вокруг одной точки, а при вращении — все точки тела движутся вокруг оси вращения.

В видеролике ниже рассказано про ускорение при криволинейном движении. Оно складывается из двух составляющих — нормальной и тангенциальной. При равномерном движении по окружности тангенциальная составляющая отсутствует, остается нормальная, которую мы в данном случае называем центростремительной.

Центростремительное ускорение

При движении по окружности модуль скорости постоянен, а вот направление скорости постоянно меняется. За изменение направления скорости отвечает центростремительное ускорение.

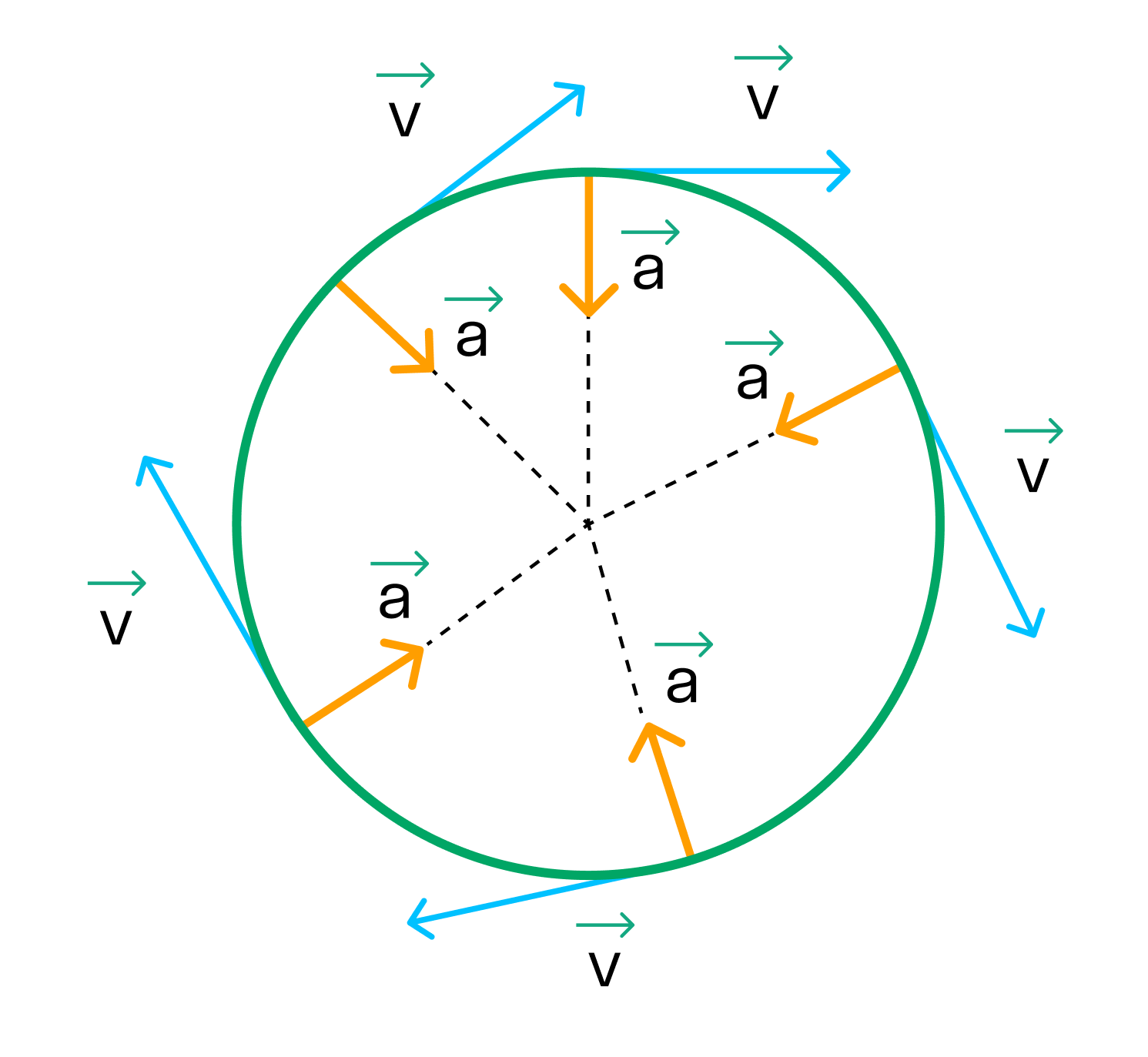
Центростремительное ускорение aц = v^2/R aц — центростремительное ускорение [м/с^2] v — скорость [м/с] R — радиус окружности

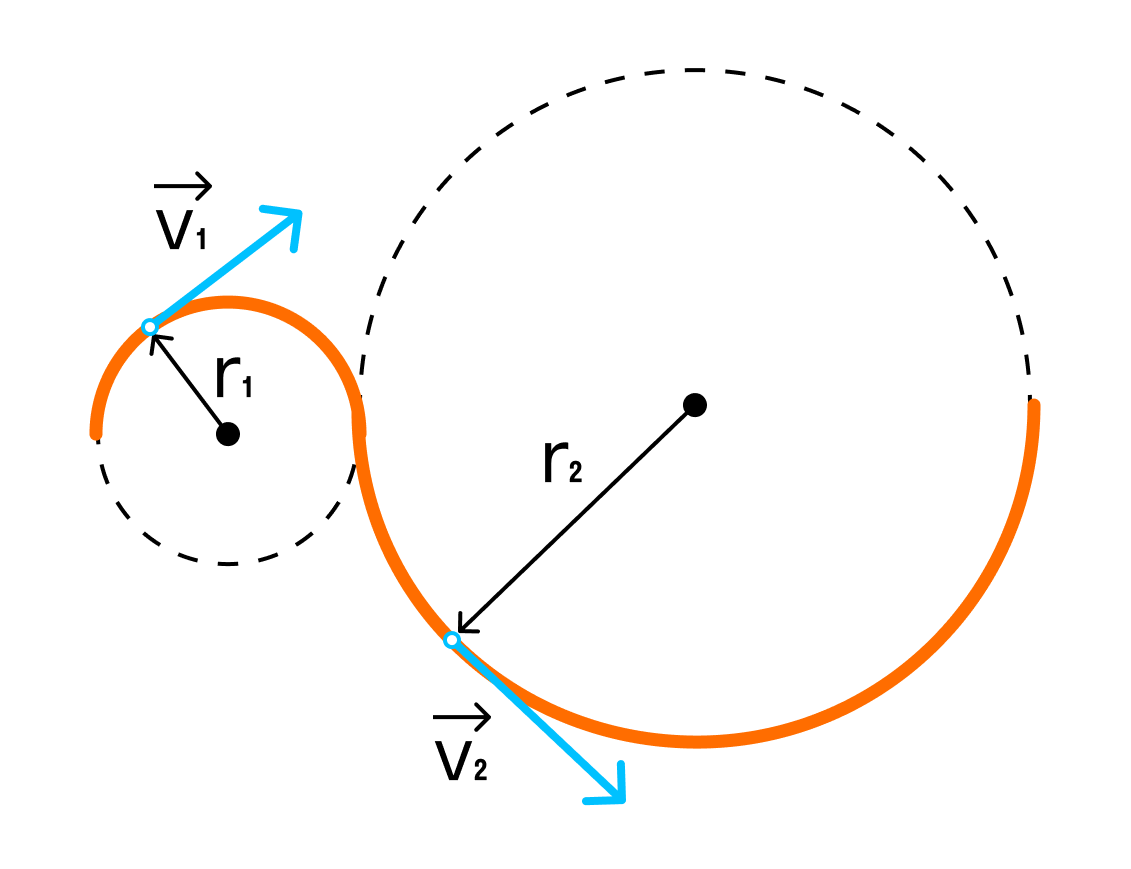
Задачка

Мотоцикл движется по закруглённому участку дороги радиусом 120 м со скоростью 36 км/ч. Чему равно центростремительное ускорение мотоцикла?

Решение:

Возьмем формулу центростремительного ускорения тела

aц = v^2/R

В условии задачи скорость дана в километрах в час, а радиус в метрах. Значит, нужно перевести скорость в м/с, чтобы избежать коллапса в решении.

36 км/с = 10 м/с

Теперь можно подставить значения в формулу:

aц = 10^2/120 = 100/120 = 10/12 ≃ 0,83 м/с^2

Ответ: центростремительное ускорение мотоциклиста равно 0,83 м/с^2

Математическое описание

Движение характеризуется различными параметрами, которые можно описать формулами и уравнениями. С точки зрения математики под термином понимается изометрия пространства в себя. При решении задач, связанных с неравномерным движением, используются следующие формулы:

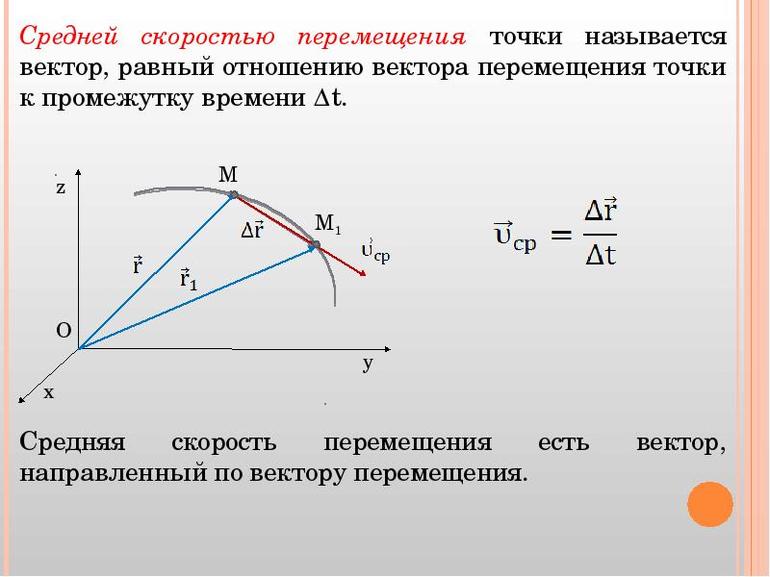
1. Вектор средней скорости. Определяется как отношение вектора изменения ко времени, за которое произошло перемещение: vср = Δs / Δt.
2. Средняя путевая скорость. Для её вычисления используется отношение пройденного пути к отрезку времени, за которое преодолено это расстояние: v ¯ = l / Δt. Более общим выражением, описывающим этот параметр, будет отношение изменения координаты объекта к промежутку времени: v = Δx / Δt.
3. Мгновенная скорость. Определяется формулой: v = lim Δs / Δt = lim Δr / Δt. При этом предел времени стремится к нулю. То есть характеристика численно равняется отношению изменения координаты ко времени, за которое оно произошло. Направление вектора параметра совпадает с траекторией движения. Следует отметить, что для прямолинейного движения скорость изменяется только по значению, а направление остаётся неизменным.
4. Равнопеременное движение. Если вектор обозначить как Δv, то изменение скорости можно обозначить как Δv = v — v0. В случае когда Δt 1 = Δt 2 = … = Δtn, тогда Δv1 = Δv2 = … = Δvn. Отсюда Δv1 / Δt1 = Δv2 / Δt2 = … = Δv3 / Δt3 = cost. Другими словами, это характеристика движения, при которой a = (v — v 0) / t.
5. Ускорение. Показывает зависимость изменения скорости от вектора к промежутку времени. Для неравномерного перемещения используется формула: a ср = Δv / Δt. Из неё следует, что мгновенное ускорение будет равняться: a = lim Δv / Δt = v’. Ускорение — это параметр, который определяется не только изменением модуля, но и вектором. Смысл заключается в том, что любое движение по окружности будет являться ускоренным из-за изменения направления в течение времени.
6. Равнопеременное перемещение. График движения описывается уравнением: v = v0 + a * t.

При расчётах довольно часто применяется закон сложения скоростей. Он позволяет определить параметр относительно зафиксированной системы отсчёта. Согласно этому способу: v2 = v1 + v. Понять справедливость утверждения можно, представив муху, ползущую по поверхности пластинки. Её скорость будет определяться относительно проигрывателя суммой движения и тем параметром, который имеет точка пластинки по отношению к площади, на которой находится в рассматриваемый момент тело.

Основные понятия и законы динамики

Часть механики, изучающая причины, вызвавшие ускорение тел, называется динамикой

Первый закон Ньютона:
Cуществуют такие системы отсчёта, относительно которых тело сохраняет свою скорость постоянной или покоится, если на него не действуют другие тела или действие других тел скомпенсировано.
Свойство тела сохранять состояние покоя или равномерного прямолинейного движения при уравновешенных внешних силах, действующих на него, называется инертностью. Явление сохранения скорости тела при уравновешенных внешних силах называют инерцией. Инерциальными системами отсчёта называют системы, в которых выполняется первый закон Ньютона.

Принцип относительности Галилея:во всех инерциальных системах отсчёта при одинаковых начальных условиях все механические явления протекают одинаково, т.е. подчиняются одинаковым законамМасса — это мера инертности телаСила — это количественная мера взаимодействия тел.

Второй закон Ньютона:Сила, действующая на тело, равна произведению массы тела на ускорение, сообщаемое этой силой:
$F{→} = m⋅a{→}$

Сложение сил заключается в нахождении равнодействующей нескольких сил, которая производит такое же действие, как и несколько одновременно действующих сил.

Третий закон Ньютона: Силы, с которыми два тела действуют друг на друга, расположены на одной прямой, равны по модулю и противоположны по направлению:
$F_1{→} = -F_2{→} $

III закон Ньютона подчёркивает, что действие тел друг на друга носит характер взаимодействия. Если тело A действует на тело B, то и тело B действует на тело
A (см. рис.).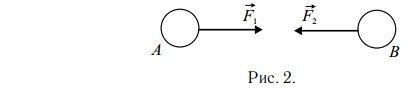
Или короче, сила действия равна силе противодействия. Часто возникает вопрос: почему лошадь тянет сани, если эти тела взаимодействуют с равными силами? Это возможно только за счёт взаимодействия с третьим телом — Землёй. Сила, с которой копыта упираются в землю, должна быть больше, чем сила трения саней о землю. Иначе копыта будут проскальзывать, и лошадь не сдвинется с места.
Если тело подвергнуть деформации, то возникают силы, препятствующие этой деформации. Такие силы называют силами упругости.

Закон Гука записывают в виде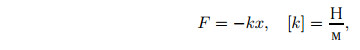
где k — жёсткость пружины, x — деформация тела. Знак «−» указывает, что сила и деформация направлены в разные стороны.

При движении тел друг относительно друга возникают силы, препятствующие движению. Эти силы называются силами трения. Различают трение покоя и трение скольжения. Сила трения скольжения подсчитывается по формуле
где N — сила реакции опоры, µ — коэффициент трения.
Эта сила не зависит от площади трущихся тел. Коэффициент трения зависит от материала, из которого сделаны тела, и качества обработки их поверхности.

Трение покоя возникает, если тела не перемещаются друг относительно друга. Сила трения покоя может меняться от нуля до некоторого максимального значенияГравитационными силами называют силы, с которыми любые два тела притягиваются друг к другу.

Закон всемирного тяготения:Весом телаСила тяжестиНевесомостьюИскусственный спутник ЗемлиПервая космическая скорость

1.3. Основные понятия и законы статики и гидростатики

устойчивое, неустойчивое и безразличное.устойчивое равновесие.неустойчивое положениебезразличное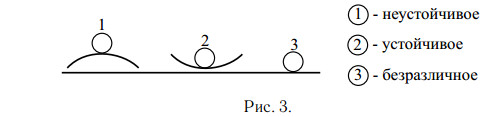Плечом силыУсловие равновесия рычага:Давлениемзакон Паскаля:Гидравлический прессA1 = A2.силой Архимедазакон Архимеда_{жидкпогр}Условие плавания тела

1.4. Законы сохранения

Импульсом телаимпульсом силы.закон сохранения импульсаМеханической работойМощностьэнергией.кинетическую и потенциальную.кинетической энергией.потенциальной энергией.Энергия сжатой пружины:механическую энергию.закон сохранения механической энергии

1.5. Механические колебания и волны

КолебаниямиГармоническими колебаниямиамплитудой колебанийПериодом TЧастотой периодических колебаний-1Математическим маятникомПериод колебаний математического маятникаПериод колебаний груза на пружинеРаспространение колебаний в упругих средах.поперечнойпродольнойДлиной волныЗвуковыми волнами

Преобразование скорости[править | править код]

Основная статья: Теорема о сложении скоростей

В классической механике Ньютона скорости преобразуются при переходе из одной инерциальной системы отсчёта в другую согласно преобразованиям Галилея. Если скорость тела в системе отсчёта S была равна v→\vec v, а скорость системы отсчёта S’ относительно системы отсчёта S равна u→\vec u, то скорость тела в при переходе в систему отсчёта S’ будет равна v′=v→−u→v’ = \vec v — \vec u.

Для скоростей, близких к скорости света преобразования Галилея становятся несправедливы. При переходе из системы S в систему S’ необходимо использовать преобразования Лоренца для скоростей:

vx′=vx−u1−(vxu)c2,vy′=vy1−u2c21−(vyu)c2,vz′=vz1−u2c21−(vzu)c2,v_x’ = \frac{v_x — u}{1-(v_x u)/c^2}, v_y’ = \frac{v_y \sqrt{1-\frac{u^2}{c^2}}}{1-(v_y u)/c^2}, v_z’ = \frac{v_z \sqrt{1-\frac{u^2}{c^2}}}{1-(v_z u)/c^2},

в предположении, что скорость u→\vec u направлена вдоль оси х системы S. Легко убедиться, что в пределе нерелятивистских скоростей преобразования Лоренца сводятся к преобразованиям Галилея.

Длина шага человека

Средняя длина поступи зависит от таких факторов как пол, рост, раса, вес, походка (манера), и может колебаться от 30 см до 1 метра. Но определена среднестатистическая длина, для мужчины она составляет 0,76 м, а средняя длина шага женщины – 0,67 м.

Поступь каждого человека имеет приблизительно одинаковую величину. Существует формула для определения средней длины шага в зависимости от роста.

Дл.Ш = P:4 + 0,37

где: Дл.Ш – длина шага (м),

P – рост.

Таким образом, средний шаг человека ростом 1,79 м составляет:

Дл.Ш = 1,79 : 4 + 0,37 = 0,82 м

Практически длину шага человека можно измерять опытным путем. Для этого необходимо отмерять участок длиной 10 метров, пройти по нему, подсчитывая количество шагов. Затем 10 м разделить на это количество, и получим длину одного.

Допустим, пешеход проделал за 10 метров 13 шагов. Получаем:

Дл.Ш = 10 : 13 = 0,77 м

Важно! В Советском Союзе было произведено определение средней длины шага. Оно составляло 1,5 метра за два, или 3 метра за четыре шага

Прямолинейное равноускоренное движение

Чтобы разобраться с тем, что за тип движения в этом заголовке, нужно ввести новое понятие — ускорение.

Ускорение — векторная физическая величина, характеризующая быстроту изменения скорости. В международной системе единиц СИ измеряется в метрах, деленных на секунду в квадрате.

СИ — международная система единиц.
«Перевести в СИ» означает перевод всех величин в метры, килограммы, секунды и другие единицы измерения без приставок. Исключение составляет килограмм с приставкой «кило».

То есть прямолинейное движение — это движение с ускорением по прямой линии, движение, при котором скорость тела меняется на равную величину за равные промежутки времени.

Уравнение движения и формула конечной скорости

Основная задача механики не поменялась по ходу текста — определение положения тела в данный момент времени. У равноускоренного движения в уравнении

Уравнение движения для равноускоренного движения x(t) — искомая координата x0 — начальная координата v0x — начальная скорость тела в данный момент времени [м/с] t — время ax — ускорение [м/с^2]

Для данного процесса также важно уметь находить конечную скорость. Это часто упрощает решение задач

Она находится по формуле

Формула конечной скорости → →v = v0 + at → v — конечная скорость тела [м/с] v0 — начальная скорость тела [м/с] t — время → a — ускорение [м/с^2]

Задача

Найдите местоположение автобуса через 0,5 часа после начала движения, разогнавшегося до скорости 60 км/ч за 3 минуты.

Решение:

Сначала найдем ускорение автобуса. Его можно выразить из формулы конечной скорости:

v = v0 + at

a = v — v0 / t

Так как автобус двигался с места, v0 = 0. Значит

a = v/t

Время дано в минутах, переведем в часы, чтобы соотносилось с единицами измерения скорости.

3 минуты = 3/60 часа = 1/20 часа = 0,05 часа

Подставим значения:

a = v/t = 60/0,05 = 1200 км/ч^2

Теперь возьмем уравнение движения.

Начальная координата равна нулю, начальная скорость, как мы уже выяснили — тоже. Значит уравнение примет вид:

x(t) = axt^2/2

Ускорение мы только что нашли, а вот время будет равно не 3 минутам, а 0,5 часа, так как нас просят найти координату в этот момент времени.

Подставим циферки:

x = 1200*0,5^2/2 = (1200*0,5^2)/2 = 150 км

Ответ: через полчаса координата автобуса будет равна 150 км.

Графики

Мы уже знаем, что такое графики функций и зачем они нужны. Для прямолинейного равноускоренного движения графики будут отличаться. Об этом — в видео ниже.

https://youtube.com/watch?v=nsFgR8rVOqE