Изохорная теплоёмкость

СТАНДАРТНЫЕ СПРАВОЧНЫЕ ДАННЫЕ

Моноксид углерода жидкий и газообразный. Плотность, энтальпия, энтропия, изохорная и изобарная теплоемкости при температурах от 70 К до 500 К и давлениях до 100 МПа

Издание официальное

Москва Стандартинформ 2021

Предисловие

• 1 РАЗРАБОТАН Главным научным метрологическим центром «Стандартные справочные данные о физических константах и свойствах веществ и материалов» (ГНМЦ «ССД»)

• 2 ВНЕСЕН Техническим комитетом по стандартизации ТК 180 «Стандартные справочные данные о физических константах и свойствах веществ и материалов»

• 3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 25 мая 2021 г. № 433-ст

• 4 ВВЕДЕН ВПЕРВЫЕ

Правила применения настоящего стандарта установлены в статье 26 Федерального закона от 29 июня 2015 г. Nt 162-ФЗ «О стандартизации в Российской Федерации». Информация об изменениях к настоящему стандарту публикуется в ежегодном (но состоянию на 1 января текущего года) информационном указателе «Национальные стандарты», а официальный текст изменений и поправок — в ежемесячном информационном указателе «Национальные стандарты». В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ближайшем выпуске ежемесячного информационного указателя «Национальные стандарты». Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования — на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет (www.gosi.ru)

Стацдартинформ. оформление. 2021

Настоящий стандарт не может быть полностью или частично воспроизведен, тиражирован и рас* пространен в качестве официального издания без разрешения Федерального агентства по техническому регулированию и метрологии

1 Область применения

2 Нормативные ссылки

3 Общие положения

4 Расширенные неопределенности расчетных значений стандартных справочных данных

по свойствам моноксида углерода

Приложение А (обязательное) Основные физические параметры и коэффициенты уравнений для определения значений стандартных справочных данных по свойствам моноксида углерода

Приложение Б (обязательное) Таблицы контрольных стандартных значений термодинамических свойств моноксида углерода на кривой насыщения

Приложение В (обязательное) Таблицы контрольных стандартных значений термодинамических свойств моноксида углерода в однофазной области

Библиография

ж W

ж

Литература

• Артемов А. В. Физическая химия. — М.: Академия, 2013. — 288 с. — (Бакалавриат). — ISBN 978-5-7695-9550-9.
• Ипполитов Е. Г., Артемов А. В., Батраков В.В. Физическая химия / Под ред. Е. Г. Ипполитова. — М.: Академия, 2005. — 448 с. — (Высшее профессиональное образование). — ISBN 978-5-7695-1456-6.
• Лифшиц Е. М. // Физическая энциклопедия / Ред. А. М. Прохоров. — М.: Большая Советская Энциклопедия, 1992. — Т. 5. — С. 77–78.
• Лифшиц Е. М. // Большая советская энциклопедия / Ред. А. М. Прохоров. — 3-е издание. — М.: Большая Советская Энциклопедия, 1976. — Т. 25. — С. 451.
• Сивухин Д. В. Общий курс физики. — Издание 5-е, исправленное. — М.: Физматлит, 2006. — Т. II. Термодинамика и молекулярная физика. — 544 с. — ISBN 5-9221-0601-5.
• // Большая российская энциклопедия. — М.: Большая российская энциклопедия, 2016. — Т. 32. — С. 54.

Краткая теория и методика выполнения работы

Удельной
теплоемкостью
вещества называется величина, равная
количеству теплоты, которую необходимо
сообщить единице массы вещества для
увеличения ее температуры на один градус
Кельвина:

. (4.1)

Теплоемкость
одного моля вещества называется молярной
теплоемкостью:

, (4.2)

где
m – масса, µ – молярная масса вещества,– число молей газа.

Значение
теплоемкости газов зависит от условий
их нагревания. В соответствии с первым
законом термодинамики количество
теплоты,
сообщенное системе, расходуется на
увеличение ее внутренней энергиии на совершение системой работыпротив внешних сил:

. (4.3)

Изменение
внутренней энергии идеального газа в
случае изменения его температурыравно:

, (4.4)

здесь
– число степеней свободы молекулы газа,
под которым подразумевается число
независимых координат, полностью
определяющих положение молекулы в
пространстве;– универсальная газовая постоянная.

При
расширении газа система совершает
работу:

. (4.5)

Если
газ нагревать при постоянном объеме
(),
тои, согласно (4.3), все полученное газом
количество теплоты расходуется только
на увеличение его внутренней энергии.
Следовательно, учитывая (4.4), молярная
теплоемкость идеального газа при
постоянном объеме будет равна:

. (4.6)

Если
газ нагревать при постоянном давление
(),
то полученное газом количество теплоты
расходуется на увеличение его внутренней
энергиии совершение газом работы:

.

Тогда
молярная теплоемкость идеального газа
при постоянном давлении определяется
следующим образом:

. (4.7)

Используя
уравнение состояния идеального газа
(уравнение Клапейрона–Менделеева),
можно показать, что для одного моля газа
справедливо соотношение:

,

поэтому:

.

Последнее выражение
называют уравнением Майера. Из него,
учитывая (4.6), получаем:

. (4.8)

Отношение
теплоемкостейобозначаюти называют показателем адиабаты или
коэффициентом Пуассона:

. (4.9)

Адиабатным
называется процесс, протекающий в
термоизолированной системе, т.е. без
теплообмена с окружающей средой,.

На
практике он может быть осуществлен в
системе, окруженной теплоизоляционной
оболочкой, но поскольку для теплообмена
необходимо некоторое время, то адиабатным
можно считать также процесс, который
протекает так быстро, что система не
успевает вступить в теплообмен с
окружающей средой.

Первый
закон термодинамики для адиабатного
процесса имеет вид.
Знак минус говорит о том, что при
адиабатном процессе система может
совершать работу только за счет внутренней
энергии. С учетом (4.4)–(4.6) имеем:

. (4.10)

Продифференцировав
уравнение Клапейрона–Менделеева,
получим:

.

Выразим
из негои подставим в формулу (4.10):

.

Выразивиз уравнения Майера и учитывая соотношение
(4.8), получим:

.

Интегрируя
данное дифференциальное уравнение при
условииполучим выражение:

.
(4.11)

Уравнение
(4.11) называется уравнением адиабаты или
уравнением Пуассона.

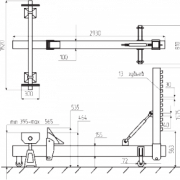
Метод
определения показателя адиабаты,
предложенный Клеманом и Дезормом (1819
г.), основывается на изучении параметров
некоторой массы газа, переходящей из
одного состояния в другое двумя
последовательными процессами –
адиабатным и изохорным. Эти процессы
на диаграмме–(рис. 4.1) изображены кривыми соответственно
1–2 и 2–3.

Если
в сосуд, соединенный с дифференциальным
датчиком давления, накачать воздух и
подождать до установления теплового
равновесия с окружающей средой, то в
этом начальном состоянии 1 газ имеет
параметры,,,
причем температура газа в сосуде равна
температуре окружающей среды,
а давлениенемного больше атмосферного.

Если
теперь на короткое время соединить
сосуд с атмосферой, то произойдет
адиабатное расширение воздуха. При этом
воздух в сосуде перейдет в состояние
2, его давление понизится до атмосферного.
Масса воздуха, оставшегося в сосуде,
которая в состоянии 1 занимала часть
объема сосуда, расширяясь, займет весь
объем.
При этом температура воздуха, оставшегося
в сосуде, понизится до.
Поскольку процесс 1–2 – адиабатный, к
нему можно применить уравнение Пуассона
(4.11):

или.

Отсюда:

. (4.12)

После
кратковременного соединения сосуда с
атмосферой охлажденный из-за адиабатного
расширения воздух в сосуде будет
нагреваться (процесс 2–3) до температуры
окружающей средыпри постоянном объеме.
При этом давление в сосуде поднимется
до.

Поскольку
процесс 2–3 – изохорный, к нему можно
применить закон Шарля:

или

. (4.13)

Из уравнений (4.12)
и (4.13) получим:

.

Прологарифмируем
это выражение:

.

Поскольку
избыточные давленияиочень малы по сравнению с атмосферным
давлением,
а также учитывая, что при,
будем иметь:

.

Откуда:

. (4.14)

Избыточные
давленияиизмеряют с помощью дифференциального
датчика давления.

Примечания и ссылки

Заметки

1. Удельный и массовый термины эквивалентны.
2. МБЫ не ставят килограмм и Кельвин в том же порядке , для символа как для имени узла (он записывает «джоуль на килограмм кельвин» , но «  Й К -1  кг -1  »), не давая д ‘объяснение . Он делает то же самое для молярной теплоемкости  : «джоуль на моль кельвин», но «  Дж  · К -1 моль -1
3. Массовый объем — величина, обратная плотности .
4. ↑ и R = 8.314 4  Дж  · К −1 моль −1 .

Рекомендации

1. .
2. Мишель Лагьер, Физика промышленных жидкостей: фундаментальные концепции и численные приложения , Technip,1996 г. , стр.  274.
3. BIPM , Международная система единиц измерения ,2019 г., 9- е  изд. , 218  с. , с.  28 год.
4. .
5. Эжен Пекле , Трактат о тепле, рассмотренный в его приложениях , Д. Аванцо и Се,1844 г., 420  с. , стр.  17Указанные значения даны в кал. Кг -1 ·  K -1 .
6. ↑ и «Энергия древесины», Технические технологии , 10 июля 2004 г., исх. BE 8535.
7. (in) в Национальном институте стандартов и технологий (по состоянию на 5 мая 2021 г. ) , «  Теплоемкость жидкости при постоянном давлении  » .

Теплоотдача и терморегуляция

Количество
теплоты Q,
переносимое вследствие теплопро­водности
за время Δt,
определяется формулой

Q=k₁ΔTΔSΔt/Δx

где
k₁—
коэффициент теплопроводности; ΔT/Δx
— градиент тем-

пературы
в направлении, перпендикулярном площадке
ΔS.

Количество
теплоты Q,
переносимое вследствие конвекции за
время Δt,
определяется формулой;

Q=k₂(T-T)ΔSΔt

где
k₂
— коэффициент теплопередачи при
конвекции; Т и Т
— соответственно
температуры поверхности ΔS
и омываемой среды.

Количество
теплоты Q,
излучаемое за время Δt
абсолютно черным телом, определяется
формулой (закон Стефана — Больцмана)

Q=σT4ΔSΔt

где
σ—
постоянная Стефана — Больцмана; Т
— абсолютная температура
тела; ΔS
— площадь излучающей поверхности тела.
Для
реальных физических тел закон Стефана
— Больцмана имеет
вид

Q=k₃σT4ΔSΔt

где
k₃
— коэффициент, учитывающий, что свойства
поверхности реальных
физических тел отличны от свойств
поверхности абсолютно
черного тела (k₃<. k>3=
1.

При
наличии двух встречных потоков радиации
от излу­чающей
поверхности к среде и от среды к
поверхности закон Стефана
— Больцмана имеет вид

Q=k₃σ(T4–T4)ΔSΔt

где
Т и Т
— абсолютные температуры тела и
среды; ΔS
— площадь
излучающей поверхности тела.

Длина
волны λ_т,
которой соответствует максимум
излуча-тельной способности черного
тела, обратно пропорциональна абсолютной
температуре Т (закон смещения Вина):

λ_m=b/T

где
b
— постоянная закона смещения Вина.

Случай твердых тел

Текущие значения

Вещество (твердая фаза)	Масса тепловой мощности ( Й К -1  кг -1 )
Асфальт	1,021
Кирпич	840
Конкретный	880
Гранит	790
Гипс	1,090
Мрамор	880
Песок	835
Стекло	720
Древесина	≈ 1200-2700

Случай кристаллизованных твердых тел

В случае твердых тел при достаточно высокой температуре применим закон Дюлонга и Пти, который позволяет, в частности, обнаружить, что при низкой температуре это происходит благодаря вкладу фононов . Если твердое тело представляет собой металл , мы должны добавить вклад электронов, который пропорционален температуре.
ПРОТИВV∼Т3{\ Displaystyle C_ {V} \ sim T ^ {3}}

Коэффициенты расширения твердых и жидких тел, как правило, достаточно низки, чтобы пренебречь разницей между C _p и C _V для большинства приложений.

Вещество	Θ{\ displaystyle \ Theta}( К )
Al	398
C (ромб)	1860
Cu	315
Fe	420
K	99
Pb	88

Согласно теории Дебая , молярная теплоемкость простого твердого тела может быть определена по формуле:

ПРОТИВV(Т)знак равно3р(4D(ты)-3тыеты-1){\ Displaystyle C_ {V} (T) = 3R \ left (4D (u) — {\ frac {3u} {\ mathrm {e} ^ {u} -1}} \ right)}

с ,
тызнак равноΘТ{\ Displaystyle и = {\ гидроразрыва {\ Theta} {T}}}

Θ{\ displaystyle \ Theta} — температура Дебая, характерная для каждого вещества,

R — молярная постоянная газов ,

и .D(ты)знак равно3ты3∫ты(Икс2+ИксеИкс-1)Икс2dИкс{\ displaystyle D (u) = {\ frac {3} {u ^ {3}}} \ int _ {0} ^ {u} \ left ({\ frac {x} {2}} + {\ frac { x} {\ mathrm {e} ^ {x} -1}} \ right) x ^ {2} \ mathrm {d} x}

Эта формула упрощается как при низкой, так и при высокой температуре; в последнем случае мы находим закон Дюлонга и Пти  :

ПРОТИВV(Т)знак равно{125π4р(ТΘ)3,если Т≪Θ3ресли Т≫Θ{\ Displaystyle C_ {V} (T) = {\ begin {cases} {\ frac {12} {5}} \ pi ^ {4} R \ left ({\ frac {T} {\ Theta}} \ right ) ^ {3}, & {\ text {si}} T \ ll \ Theta \\ 3R & {\ text {si}} T \ gg \ Theta \ end {case}}}

Теория больше не действительна для составных тел.

Эмпирические формулы

Для чистых веществ (твердых, жидких или газообразных) и при постоянном давлении могут быть определены две эмпирические формулы с тремя параметрами для заданного температурного интервала:

ПРОТИВпзнак равнов+бТ+противТ2{\ displaystyle C_ {p} = a + bT + cT ^ {2}}или иначе .ПРОТИВпзнак равнов′+б′Т+против′Т-2{\ displaystyle C_ {p} = a ‘+ b’T + c’T ^ {- 2}}

Значения коэффициентов указаны в таблицах и характерны для данного тела.

Например, для сухой древесины:

противп,внетчасуdрезнак равно0,1031+0,003867Т{\ displaystyle c_ {p, безводный} = 0 {,} 1031 + 0 {,} 003 \, 867 \, T}

с участием:

• противп,внетчасуdре{\ displaystyle c_ {p, безводный}} : выражается в кДж · K −1  кг −1
• T  : термодинамическая температура ( K ).

При 20  ° C для сухой древесины получается 1236 Дж ·  К -1  кг -1 .

Для влажной древесины:

противп,частымяdезнак равно100противп,внетчасуdре+ЧАСsпротивп,евты100+ЧАСs{\ displaystyle c_ {p, wet} = {\ frac {100 \, c_ {p, безводный} + Hs \, c_ {p, вода}} {100 + Hs}}}

где Hs — масса воды по отношению к массе сухой древесины в%.

Воздух — идеальный газ

Прежде чем раскрывать вопрос теплоемкости воздуха, рассмотрим модель идеального газа. В соответствии с ней полагают, что система состоит из невзаимодействующих друг с другом частиц, которые хаотично движутся в ограниченном объеме пространства. Скорости частиц подчиняются классическому распределению Максвелла-Больцмана. Модель также предполагает, что частицы являются безразмерными.

Насколько точно в приведенную модель вписывается воздушная смесь? Известно, что воздух состоит в основном из молекул азота и кислорода. Эти молекулы являются химически нейтральными. Существующие между ними ван-дер-ваальсовые взаимодействия являются очень слабыми, поэтому их при выполнении термодинамических расчетов можно не учитывать. Что касается размеров молекул, то ими также можно пренебречь, так как расстояния между ними на несколько порядков больше. Таким образом, воздух очень хорошо описывается моделью идеального газа.

Таблица удельной теплоемкости пищевых продуктов

В таблице приведены значения средней удельной теплоемкости пищевых продуктов (овощей, фруктов, мяса, рыбы, хлеба, вина и т. д.) в диапазоне температуры 5…20°С и нормальном атмосферном давлении.

Таблица удельной теплоемкости продуктов питания

Продукты	C, Дж/(кг·К)
Абрикосы	3770
Ананасы	3684
Апельсины	3730
Арбуз	3940
Баклажаны	3935
Брюква	3810
Ветчина	2140
Вино крепленое	3690
Вино сухое	3750
Виноград	3550
Вишня	3650
Говядина и баранина жирная	2930
Говядина и баранина маложирная	3520
Горох	3684
Грибы свежие	3894
Груши	3680
Дрожжи прессованные	1550…3516
Дыни	3850
Ежевика	3642
Земляника	3684
Зерно пшеничное	1465…1549
Кабачки	3900
Капуста	3940
Картофель	3430
Клубника	3810
Колбасы	1930…2810
Крыжовник	3890
Лимоны	3726
Лук	2638
Макароны не приготовленные	1662
Малина	3480
Мандарины	3770
Маргарин сливочный	2140…3182
Масло анисовое	1846
Масло мятное	2080
Масло сливочное	2890…3100
Масло сливочное топленое	2180
Мед	2300…2428
Молоко сухое	1715…2090
Морковь	3140
Мороженое (при -10С)	2175
Мука	1720
Огурцы	4060
Пастила	2090
Патока	2512…2700
Перец сладкий	3935
Печенье	2170
Помидоры	3980
Пряники	1800…1930
Редис	3970
Рыба жирная	2930
Рыба нежирная	3520
Салат зеленый	4061
Сало топленое	2510
Сахар кусковой	1340
Сахарный песок	720
Свекла	3340
Свинина жирная	260
Свинина нежирная	3010
Слива	3750
Сметана	3010
Смородина черная	3740
Сода	2256
Соль поваренная (2% влажности)	920
Спаржа	3935
Сыр жирный	2430
Творог	3180
Телятина жирная	3180
Телятина нежирная	3520
Тесто заварное	2910
Тыква	3977
Хлеб (корка)	1680
Хлеб (мякиш)	2800
Черешня	3770
Чернослив	3181
Чеснок	3140
Шоколад	2340…2970
Шпинат	3977
Яблоки	3760
Яйцо куриное	3180

Кроме таблиц удельной теплоемкости, вы также можете ознакомиться с подробнейшей таблицей плотности веществ и материалов, которая содержит данные по величине плотности более 500 веществ (металлов, пластика, резины, продуктов, стекла и др.).

1. Исаченко В. П., Осипова В. А., Сукомел А. С. Теплопередача. Учебник для вузов, изд. 3-е, перераб. и доп. — М.: «Энергия», 1975.
2. Тепловые свойства металлов и сплавов. Справочник. Лариков Л. Н., Юрченко Ю. Ф. — Киев: Наукова думка, 1985. — 439 с.
3. Физические величины. Справочник. А. П. Бабичев, Н. А. Бабушкина, А. М. Братковский и др. Под ред. И. С. Григорьева — М.: Энергоатомиздат, 1991. — 1232 с.
4. Еремкин А. И., Королева Т. И. Тепловой режим зданий: Учебное пособие. — М.: Издательство ACB, 2000 — 368 с.
5. Кириллов П. Л., Богословская Г. П. Тепломассобмен в ядерных энергетических установках: Учебник для вузов.
6. Михеев М. А., Михеева И. М. Основы теплопередачи. Изд. 2-е, стереотип. М.: «Энергия», 1977. — 344 с. с ил.
7. Казанцев Е. И. Промышленные печи. Справочное руководство для расчетов и проектирования.
8. Франчук А. У. Таблицы теплотехнических показателей строительных материалов, М.: НИИ строительной физики, 1969 — 142 с.
9. Добрынин В. М., Вендельштейн Б. Ю., Кожевников Д. А. Петрофизика: Учеб. для вузов. 2-ое изд. перераб. и доп. под редакцией доктора физико-математических наук Д. А. Кожевникова — М.: ФГУП Издательство «Нефть и газ» РГУ нефти и газа им. И.М. Губкина, 2004. — 368 с., ил.
10. В. Блази. Справочник проектировщика. Строительная физика. М.: Техносфера, 2005. — 536 с.
11. Енохович А. С. Справочник по физике. М.: «Просвещение», 1978. — 415 с. с ил.
12. Строительная теплотехника СНиП II-3-79. Минстрой России — Москва 1995.
13. Мустафаев Р. А. Теплофизические свойства углеводородов при высоких параметрах состояния. М.: Энергоатомиздат, 1991. — 312 с.
14. Новиченок Н. Л., Шульман З. П. Теплофизические свойства полимеров. Минск, «Наука и техника» 1971. — 120 с.
15. Шелудяк Ю. Е., Кашпоров Л. Я. и др. Теплофизические свойства компонентов горючих систем. М., 1992. — 184 с.

Идеальный газ

Идеальным называется такой газ, частицы которого считаются материальными точками, то есть не имеют размеров, но обладают массой, и у которого вся внутренняя энергия состоит исключительно из кинетической энергии движения молекул и атомов.

Любой реальный газ в идеале никогда не будет удовлетворять описанной модели, поскольку его частицы все же имеют некоторые линейные размеры и взаимодействуют между собой с помощью слабых ван-дер-ваальсовых связей или химических связей другого типа. Однако при низких давлениях и высоких температурах расстояния между молекулами велики, а их кинетическая энергия превышает потенциальную в десятки раз. Все это позволяет применять с высокой степенью точности идеальную модель для реальных газов.

Теплоемкость и ее виды

Согласно физическому определению, теплоемкость — это величина, показывающая, сколько нужно на систему затратить теплоты, чтобы ее нагреть на 1 градус Цельсия или на 1 кельвин. Поскольку процессы нагревания и охлаждения являются обратимыми, то при охлаждении системы на 1 градус выделяется количество теплоты, равное ее теплоемкости.

Как физическая величина теплоемкость может быть абсолютной, молярной или массовой. Определение абсолютной теплоемкости для произвольной системы было дано выше. Молярной называется теплоемкость на 1 моль газа, массовой — на 1 кг газа. Молярная величина чаще используется для рассматриваемого агрегатного состояния материи.

В зависимости от изопроцесса, при котором измеряют теплоемкость, она бывает изохорной и изобарной. В первом случае в системе с газом не изменяется объем, во втором случае сохраняется давление.

Формулы изохорной и изобарной теплоемкостей воздуха

Сначала рассмотрим изохорную величину. Обозначим ее C_V. Первое начало термодинамики, которое следует из закона сохранения энергии, для изохорного процесса выглядит следующим образом:

То есть все тепло H, подводимое к системе, идет на увеличение ее внутренней энергии. Изменение величины U можно записать так:

С другой стороны, если воспользоваться универсальным уравнением состояния идеальной газовой системы, то формула для dU запишется в виде:

Здесь z — количество степеней свободы молекул, n — количество вещества, R — постоянная, dT — изменение температуры. Выражение выше следует из того факта, что внутренняя энергия идеального газа в точности равна кинетической энергии его молекул.

Из сравнения двух равенств получаем формулу для изохорной теплоемкости:

В случае воздуха z=5, поскольку он на 99 % состоит из двухатомных молекул азота и кислорода (двухатомные молекулы имеют 3 поступательные и 2 вращательные степени свободы). Полагая n=1 моль, приходим к формуле изохорной молярной теплоемкости воздуха:

Напомним, что постоянная R равна 8,314, тогда C_V = 20,785 Дж/(моль*К).

Теперь определим молярную изобарную теплоемкость воздуха. Поскольку в результате изобарного нагрева газ расширяется, то он выполняет некоторую работу. Первое начало термодинамики в этом случае принимает вид:

Энтальпия H через изобарную теплоемкость C_P для 1 моль вещества запишется так:

Работу газа с использованием уравнения Клапейрона-Менделеева можно записать так:

Эти выражения позволяют записать следующее соотношение изобарной и изохорной теплоемкостей:

Подставляя величину C_V для воздуха, получаем изобарную молярную теплоемкость для него:

Таким образом, величина C_P оказывается больше, чем C_V.

Максимальная и минимальная теплоты процесса

Уравнения первого закона термодинамики
в сложных закрытых ТС при двух фиксированных
параметрах имеют вид:

— для изохорно-изотермического процесса
(T,V=const):ℒ_Т,V;

— для изобарно-изотермического процесса
(T,p=const):
ℒ_Т,р.

При написании этих уравнений использовалось
правило знаков, принятое в термодинамике,
т.е.,
если теплота подводится к ТС, иℒ>0,
если работа совершается термодинамической
системой. В термохимии принято
противоположное правило знаков для
теплоты, т.е. теплота,
(положительна), если она отводится от
ТС. Тогда для конечных процессов 1-2
уравнение 1-го закона термодинамики
будет иметь вид:

ℒ_Т,V, (1)

ℒ_Т,р, (2)

Соотношения (1) и (2) справедливы для любых
процессов, обратимых и необратимых.

Для обратимого процесса
ℒ=ℒ_max ,:

ℒ_Т,Vmax, (3)

ℒ_Т,pmax, (4)

Для максимально возможного необратимого
процесса ℒ=ℒ_min=0,:

, (5)

.(6)

Соотношения (5) и (6) используются в
химической термодинамике для расчета
изохорного и изобарного тепловых
эффектов химических реакций (ТЭХР). В
этом случае работа ℒ_maxпреобразуется в тепловую энергию
неупорядоченного движения частиц (в
теплотуи).

В случае обратимого равновесного
процесса перераспределения масс
(уравнения (3) и (4)) величиныи— это количества теплоты, которыми ТС
обменивается с окружающей средой в
процессахи.ℒ_Т,Vmaxиℒ_Т,pmax— максимальные количества работы
немеханического характера, которые
могут быть получены от ТС в процессахи.

В случае необратимого процесса
перераспределения массы в соответствии
со вторым законом термодинамики работаℒ_maxпреобразуется в теплоту, количество
которого равно изменению внутренней
энергиив процессе,
или изменению энтальпиив процессе,
протекающем в сложных термодинамических
системах.

Химические реакции, при которых теплота
отводится от термодинамической системы,
чтобы конечные продукты имели ту же
температуру, что и начальные реагенты,
называются экзотермическими химическими
реакциями. Химические реакции,
сопровождающиеся поглощением теплоты,
приT=const, называются эндотермическими химическими
реакциями.

Рассмотрим два примера: 1. разрядка
химического источника электроэнергии
(аккумулятор, батарея карманного фонаря)
– процесс обратимый: ℒ_Т,pmax— преобразуется в электрическую энергию,
а— отводится от системы. 2. Если замкнуть
клеммы батареи накоротко, то получим
максимально необратимый процесс:ℒ,.

Изопроцессы в газах

Определение 2

Чаще всего рассматриваются два значения теплоемкости газов: 

• CV являющаяся молярной теплоемкостью в изохорном процессе (V=const);
• Cp представляющая собой молярную теплоемкость в изобарном процессе (p=const).

При условии постоянного объема газ не совершает работы: A=. Исходя из первого закона термодинамики для 1 моля газа, можно сказать, что справедливым является следующее выражение: 

QV=CV∆T=∆U.

Изменение величины ΔU внутренней энергии газа прямо пропорционально изменению значения ΔT его температуры.

В условиях процесса при постоянном давлении первый закон термодинамики дает такую формулу: 

Qp=∆U+p(V2-V1)=CV∆T+pV.

В котором ΔV является изменением объема 1 моля идеального газа при изменении его температуры на ΔT. Таким образом, можно заявить, что: 

Cp=Qp∆T=CV+p∆V∆T.

Из уравнения состояния идеального газа, записанного для 1 моля, может выражаться отношение ΔVΔT: 

pV=R.

В котором R представляет собой универсальную газовую постоянную. При условии постоянства давления p=const, можно записать следующее:p∆V=R∆T или ∆V∆T=Rp.

Определение 3

Из этого следует, что выражающее связь между молярными теплоемкостями Cp и CVсоотношение имеет вид (формула Майера): 

Cp=CV+R.

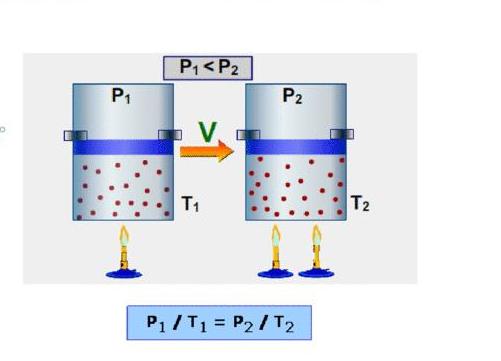
В процессе с неизменным давлением молярная теплоемкость Cp газа всегда превышает молярную теплоемкость CV в процессе с не подверженным изменениям объемом, что демонстрируется на рисунке 3.10.1.

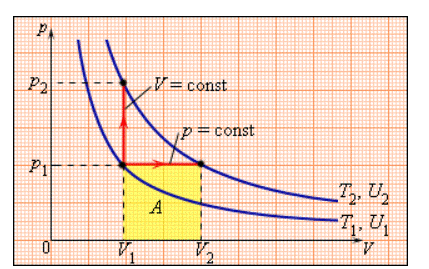
Рисунок 3.10.1. Два возможных процесса нагревания газа на ΔT=T2 –T1. При p=const газ совершает работу A=p1(V2 – V1). Поэтому Cp>CV.

Определение 4

Отношение теплоемкостей в процессах с постоянным давлением и постоянным объемом занимает важное место в термодинамике и обозначается в виде греческой буквы γ. 

γ=CpCV.

Данное отношение включено в формулу для адиабатического процесса.

Между двумя изотермами, обладающими температурами T1 и T2 на диаграмме (p, V) реальны различные варианты перехода. Так как для всех подобных переходов изменение величины температуры ΔT=T2 –T1 является одним и тем же, выходит, что изменение значенияΔU внутренней энергии тоже одинаково. С другой стороны, совершенные при этом работы A и количества теплоты Q, полученные в результате теплообмена, выйдут разными для различных путей перехода. Из этого следует, что газа имеет относительно приближенное к бесконечности число теплоемкостей. Cp и CV представляют собой частные, однако, очень важные для теории газов, значения теплоемкостей.

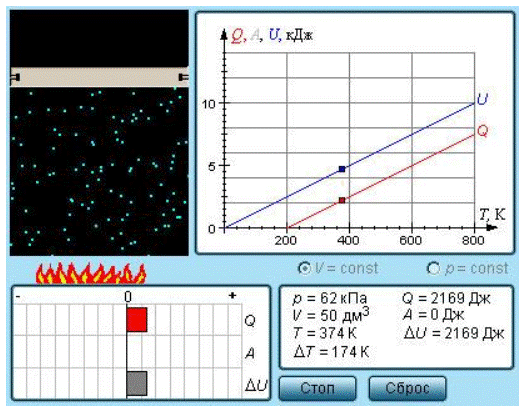
Рисунок 3.10.2. Модель теплоемкости идеального газа.

Определение 5

Термодинамические процессы, в которых теплоемкость газа не подвергается изменениям, носят название политропических.

Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!

Описать задание

Каждый изопроцесс являются политропическим. В изотермическом процессе ΔT=, из-за чего CT=∞. В адиабатическом процессе ΔQ=, выходит, что Cад=.

Замечание 1

Стоит обратить внимание на то, что «теплоемкость» и «количество теплоты» являются крайне неудачными терминами, доставшимися современной науке в качестве наследства теории теплорода, которая господствовала в XVIII веке. Данная теория представляла теплоту в виде содержащегося в телах особого невесомого вещества

Считалось, что оно не подвержено уничтожению и не может быть созданным. Явление нагрева объясняли повышением, а охлаждение – понижением содержания в телах теплорода. Однако теория теплорода оказалась несостоятельной, так как не смогла дать ответа на вопрос, почему одинаковое изменение внутренней энергии тела возможно получить, приводя ему разное количество теплоты в зависимости от совершаемой им работы. По этой причине утверждение, что в данном теле содержится некоторый запас теплорода лишено смысла

Данная теория представляла теплоту в виде содержащегося в телах особого невесомого вещества. Считалось, что оно не подвержено уничтожению и не может быть созданным. Явление нагрева объясняли повышением, а охлаждение – понижением содержания в телах теплорода. Однако теория теплорода оказалась несостоятельной, так как не смогла дать ответа на вопрос, почему одинаковое изменение внутренней энергии тела возможно получить, приводя ему разное количество теплоты в зависимости от совершаемой им работы. По этой причине утверждение, что в данном теле содержится некоторый запас теплорода лишено смысла.

Плотность воздуха в зависимости от температуры

Представлена подробная таблица значений плотности воздуха в сухом состоянии при различных температурах и нормальном атмосферном давлении. Чему равна плотность воздуха? Аналитически определить плотность воздуха можно, если разделить его массу на объем, который он занимает
при заданных условиях (давление, температура и влажность). Также можно вычислить его плотность по формуле уравнения состояния идеального газа . Для этого необходимо знать абсолютное давление и температуру воздуха, а также его газовую постоянную и молярный объем. Это уравнение позволяет вычислить плотность воздуха в сухом состоянии.

На практике, чтобы узнать какова плотность воздуха при различных температурах
, удобно воспользоваться готовыми таблицами. Например, приведенной таблицей значений плотности атмосферного воздуха в зависимости от его температуры. Плотность воздуха в таблице выражена в килограммах на кубический метр и дана в интервале температуры от минус 50 до 1200 градусов Цельсия при нормальном атмосферном давлении (101325 Па).

t, °С	ρ, кг/м 3	t, °С	ρ, кг/м 3	t, °С	ρ, кг/м 3	t, °С	ρ, кг/м 3
-50	1,584	20	1,205	150	0,835	600	0,404
-45	1,549	30	1,165	160	0,815	650	0,383
-40	1,515	40	1,128	170	0,797	700	0,362
-35	1,484	50	1,093	180	0,779	750	0,346
-30	1,453	60	1,06	190	0,763	800	0,329
-25	1,424	70	1,029	200	0,746	850	0,315
-20	1,395	80	1	250	0,674	900	0,301
-15	1,369	90	0,972	300	0,615	950	0,289
-10	1,342	100	0,946	350	0,566	1000	0,277
-5	1,318	110	0,922	400	0,524	1050	0,267
1,293	120	0,898	450	0,49	1100	0,257
10	1,247	130	0,876	500	0,456	1150	0,248
15	1,226	140	0,854	550	0,43	1200	0,239

При 25°С воздух имеет плотность 1,185 кг/м 3 .
При нагревании плотность воздуха снижается — воздух расширяется (его удельный объем увеличивается). С ростом температуры, например до 1200°С, достигается очень низкая плотность воздуха, равная 0,239 кг/м 3 , что в 5 раз меньше ее значения при комнатной температуре. В общем случае, снижение при нагреве позволяет проходить такому процессу, как естественная конвекция и применяется, например, в воздухоплавании.

Если сравнить плотность воздуха относительно , то воздух легче на три порядка — при температуре 4°С плотность воды равна 1000 кг/м 3 , а плотность воздуха составляет 1,27 кг/м 3 . Необходимо также отметить значение плотности воздуха при нормальных условиях. Нормальными условиями для газов являются такие, при которых их температура равна 0°С, а давление равно нормальному атмосферному. Таким образом, согласно таблице, плотность воздуха при нормальных условиях (при НУ) равна 1,293 кг/м 3
.

Тепловые машины. Формула КПД в термодинамике

Тепловая машина, в простейшем случае, состоит из нагревателя, холодильника и рабочего тела. Нагреватель сообщает тепло рабочему телу, оно совершает работу, затем охлаждается холодильником, и все повторяется вновь. Типичным примером тепловой машины является двигатель внутреннего сгорания.

Коэффициент полезного действия тепловой машины вычисляется по формуле

Вот мы и собрали основные формулы термодинамики, которые пригодятся в решении задач. Конечно, это не все все формулы из темы термодинамика, но их знание действительно может сослужить хорошую службу. А если возникнут вопросы  – помните о студенческом сервисе, специалисты которого готовы в любой момент прийти на выручку.

Теплоемкость.

Теплоемкость – свойство материала поглощать определенное количество тепла при нагревании и выделять его при охлаждении.

Удельная теплоемкость – количество тепла, необходимое для нагревания единицы количества вещества на один градус.

Формула для расчёта удельной теплоёмкости (или табл.знач.):

,

где — удельная теплоёмкость,

— количество теплоты, полученное веществом при нагреве (или выделившееся при охлаждении),

— масса нагреваемого (охлаждающегося) вещества,

— разность конечной и начальной температур вещества.

В зависимости от единиц измерения количества вещества различают:

· массовую теплоемкость С , Дж / (кг К) — это количество теплоты, которое необходимо подвести к единице массы вещества, чтобы нагреть его на единицу температуры;

· объемную теплоемкость С’, Дж / (м3 К) — это количество теплоты, которое необходимо подвести к единице объёма вещества, чтобы нагреть его на единицу температуры;

· мольную теплоемкость С_М , Дж / (кмоль К) — это количество теплоты, которое необходимо подвести к 1 молю вещества, чтобы нагреть его на единицу температуры.

Между различными видами теплоемкостей существует следующая зависимость:

С’ = С_М/22,4 ; С = С_М/М ; С = С’/ρ .

Различают среднюю (С_m) и истинную (С) теплоемкость:

С_m = q_1-2/(t₂–t₁) , С = lim(q/t)=dq/dt=dq/dT,

где q_1-2 – теплота, подводимая к газу в процессе нагревания от температуры t₁ до температуры t₂ .

Истинная теплоемкость – первая производная от количества теплоты, подводимой в процессе нагрева к телу, по его температуре.

Теплоемкость газа не постоянна. Она зависит от температуры и давления. Влияние давления на теплоемкость газов незначительное, поэтому обычно учитывают только влияние температуры.

Зависимости средней теплоемкости от температуры:

если тело нагревается от 0 до некоторой температуры t: С_m =a+bt/2;

если тело нагревается от температуры t₁ до температуры t₂: С_m =a+b(t₁+t₂),

где a, b, – коэффициенты, зависящие от природы газа, определяются экспериментально и приводятся в справочных таблицах.

Теплоемкость зависит от способа подвода теплоты к газу. Чаще всего используют 2 способа:

при V = const ( изохорный процесс ) — C_v;

при P = const ( изобарный процесс ) — С_р.

Теплоемкости при постоянном давлении и постоянном объеме связаны между собой следующими соотношениями:

С_р = C_v + R – уравнение Майера; С_р / C_v = к , (1)

где R — газовая постоянная, Дж /( кг К);

к — показатель адиабаты , зависит от количества атомов в молекуле газа: для одноатомных газов — к = 1,66; для двухатомных газов — к = 1,4; для трех- и многоатомных — к = 1,33 .

Анализ уравнений (1) показывает, что во время нагревания газа при P=const затрачивается тепла больше, чем при V=const.

Значение теплоемкости приближенно можно рассчитать следующим образом:

C_V= R / (к — 1) ; C_P= к R / (к – 1).

Массовую Ссм и объемную С’см теплоемость газовых смесей определяют по формулам:

C_см = Σ (C_i g_i ) ; C’_см= Σ (C’_i r_i ) ,

где C_i– массовая теплоемкость отдельного газа, Дж/(кгК);

g_i– массовые доли газов, составляющих смесь;

C’_i– объемная теплоемкость отдельного газа, Дж/(м3К);

r_i– объемные доли газов, составляющих смесь.

Количество теплоты, необходимое на нагрев тела, можно определить следующим образом:

Q = mС(t₂-t₁),

где С – удельная теплоемкость вещества.

Рассмотрим пример:

Газ (воздух) нагревается от начальной температуры t₁=25oC до t₂=130oC, масса газа m=21кг. Определить количество подведенного к воздуху тепла Q, считая удельную теплоемкость воздуха постоянной с=const=1,0301 кДж/кг·К. Выразить количество теплоты Q в килокалориях (ккал).

Решение:

Q = mС(t₂-t₁)=21·1,0301·(130-25)=2271 кДж·0,239=542,769ккал.

Ответ: Q = 2271 кДж=542,769ккал.