Гидрология

Поверхностное натяжение

Часто, получив задание: «Назвать свойства жидкостей», сразу запоминают поверхностное натяжение. Ведь детей с ними знакомят на уроках физики, химии и биологии. И каждый испытуемый со своей стороны объясняет этот важный параметр.

Классическое определение поверхностного натяжения следующее: это интерфейс. То есть в момент, когда жидкость заняла определенный объем, она граничит снаружи с газовой средой: воздухом, паром или каким-либо другим веществом. Следовательно, разделение фаз происходит в точке контакта.

В этом случае молекулы стремятся окружить себя как можно большим количеством частиц и, следовательно, как бы приводят к сжатию жидкости как целого. В результате поверхность выглядит удлиненной. Это свойство также может объяснить сферическую форму жидких капель в отсутствие силы тяжести. Действительно, именно такая форма идеальна с точки зрения энергии молекулы. Примеры:

• капли жидкости в невесомости.
• кипящая вода;
• пузырь;

Некоторые насекомые приспособились «ходить» по поверхности воды именно благодаря поверхностному натяжению. Примеры: водяные ястребы, водяные жуки, некоторые личинки.

Коэффициент – объемное расширение – вода

Коэффициент объемного расширения воды меняется с температурой гораздо сильнее, чем ртути, так что равномерность ртутной шкалы много больше, чем у воды. Таким образом, по сравнению с водяным термометром Галилея pry гний термометр Гюйгенса является весьма большим усовершенствованием, не потерявшим своего значения и до настоящего времени.
 

Коэффициент объемного расширения воды сильно зависит от температуры, а в интервале от О до 4 С принимает отрицательное значение.
 

Коэффициент объемного расширения воды а при 4 С меняет знак, будучи при 0 / 4 С величиной отрицательной.
 

Опыт показывает, что коэффициент объемного расширения воды гораздо больше, чем льда. Возможно, что молекулы Н2О, перешедшие в полости структуры льда, несколько расширяют тетраэдрический каркас изнутри. Разрушение тетраэдрической структуры воды происходит не при нагревании, но и при сжатии. При этом увеличение давлен ствует на структуру воды в том же направлении, что и повышение температуры. При высоком давлении возникает более плотная структура, отличная от тетраэдрической.
 

РВ, РК – коэффициенты объемного расширения воды и керосина.
 

Рвт – коэффициент деформации пустот; – коэффициент объемного расширения воды; Др – снижение давления в водоносной зоне.
 

В интервале температур 0 t 4 C коэффициент объемного расширения воды отрицательный. Доказать, что в этом интервале температур при адиабатическом сжатии вода охлаждается.
 

В интервале температур 0 t 4 С коэффициент объемного расширения воды отрицательный. Доказать, что в этом интервале температур при адиабатном сжатии вода охлаждается.
 

Увеличение объема воды при ее нагревании пропорционально коэффициенту объемного расширения воды ( 0 0006), степени нагрева Д / и количеству нагреваемой воды.
 

ЛГГ – – Го; рв, РК – коэффициенты объемного расширения воды и керосина.
 

Температурный коэффициент объемного расширения жидкости слабо зависит от температуры. Коэффициент объемного расширения воды сильно зависит от температуры, а в интервале от 0 до 4 С принимает отрицательное значение.
 

Сжиженный газ обладает большим коэффициентом объемного расширения. Коэффициент объемного расширения пропана в 16 раз превышает коэффициент объемного расширения воды.
 

Сжиженный газ имеет весьма значительный коэффициент объемного расширения. Например, коэффициент объемного расширения пропана в 16 раз превышает коэффициент объемного расширения воды.
 

Газообразные углеводороды имеют плотность, значительно превышающую плотность воздуха, отличаются медленной диффузией в атмосфере ( особенно при отрицательных температурах воздуха), низкими пределами взрываемости ( воспламеняемости) в воздухе, невысокой температурой воспламенения по сравнению с другими горючими газами, возможностью образования конденсата при снижении температуры до точки росы или при повышении давления. В сжиженном состоянии эти газы имеют высокий коэффициент объемного расширения, превышающий коэффициент объемного расширения воды, значительную упругость паров, возрастающую с ростом температуры. Сжиженные газы охлаждаются до отрицательных температур и при определенных условиях обладают вредными для здоровья человека свойствами.
 

Сжиженные газы в отличие от большинства жидкостей имеют очень высокий коэффициент объемного расширения. Например, коэффициент объемного расширения многих сжиженных газов примерно в десять раз больше коэффициента объемного расширения воды.
 

8.2 Реальный газ

Относительнуюплотностьреальногогазавычисляютпоформуле

где

d (t, р) -относительнаяплотностьреальногогаза;

Z_air(t, p) -коэффициентсжимаемостисухоговоздухастандартногосостава;

Z_mix(t, p) -коэффициентсжимаемостигаза.

КоэффициентсжимаемостиZ_mix(t, p) вычисляютпоформуле (), сиспользованиемзначенийкоэффициентовсуммирования , приведенныхдляиндивидуальныхчистыхвеществв (). КоэффициентсжимаемостиZ_air(t, p) приведенв ():

Z_air (273,15 К, 101,325 кПа) = 0,99941;

Z_air (288,15 К, 101,325 кПа) = 0,99958;

Z_air (293,15 К, 101,325 кПа) = 0,99963.

Плотностьреальногогазавычисляютпоформуле

где

ρ (t, p) -плотностьреальногогаза.

ЧислоВоббереальногогазавычисляютпоформуле

где

W-числоВоббереальногогаза;

-вычисляютпоформуле ().

Примечание 16 -Требуетсяопределеннаявнимательностьприпримененииединицизмеренияпри
вычислениях, приведенныхвнастоящемподразделе, особеннопривычисленияхплотности. ПриR, выраженнойв джоуляхнамоль-кельвин, р-вкилопаскаляхиМ-вкилограммахнакиломоль, значениеρавтоматическиполучаетсявкилограммахнакубическийметр-эторекомендуемаяединицаСИ.

Давление в жидкости

Нормальная сила F называется силой давления и вызывает в жидкости нормальные напряжения сжатия, которые определяются отношением:

Нормальные напряжения, возникающие в жидкости под действием внешних сил, называются гидромеханическим давлением или просто давлением.

Системы отсчета давления

Рассмотрим системы отсчета давления. Важным при решении практических задач является выбор системы отсчета давления (шкалы давления). За начало шкалы может быть принят абсолютный нуль давления. При отсчете давлений от этого нуля их называют абсолютными — P_абс.

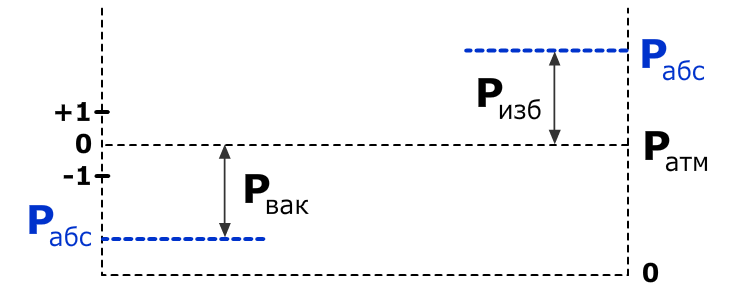
Однако, как показывает практика, технические задачи удобнее решать, используя избыточные давления P_изб, т.е. когда за начало шкалы принимается атмосферное давление.

Давление, которое отсчитывается «вниз» от атмосферного нуля, называется давлением вакуума P_вак, или вакуумом.

где P_атм — атмосферное давление, измеренное барометром.

Связь между абсолютным давлением P_абс и давлением вакуума P_вак можно установить аналогичным путем:

И избыточное давление, и вакуум отсчитываются от одного нуля (P_атм), но в разные стороны.

Таким образом, абсолютное, избыточное и вакуумное давления связаны и позволяют пересчитать одно в другое.

Единицы измерения давления

Практика показала, что для решения технических (прикладных) задач наиболее удобно использовать избыточные давления. Основной единицей измерения давления в системе СИ является паскаль (Па), который равен давлению, возникающему при действии силы в 1 Н на площадь размером 1 м2 (1 Па = 1 Н/м2).

Однако чаще используются более крупные единицы: килопаскаль (1 кПа = 103 Па) и мегапаскаль (1 МПа = 106 Па).

В технике широкое распространение получила внесистемная единица — техническая атмосфера (ат), которая равна давлению, возникающему при действии силы в 1 кгс на площадь размером 1 см2 (1 ат = 1 кгс/см2).

Соотношения между наиболее используемыми единицами следующие:

10 ат = 0,981 МПа ≈ 1 МПа или 1 ат = 98,1 кПа ≈ 100 кПа.

В зарубежной литературе используется также единица измерения давления бар

(1 бар = 105 Па).

В каких ещё единицах измеряется давление, можно посмотреть здесь

Рассмотрим некоторые свойства жидкостей, которые оказывают наиболее существенное влияние на происходящие в них процессы и поэтому учитываются при расчетах гидравлических систем.

8.1 Идеальный газ

Относительнаяплотностьидеальногогазанезависитотвыборастандартногосостояния, иеевычисляютпоформуле

где

d°-относительнаяплотностьидеальногогаза;

M_j-молярнаямассаj-гокомпонента;

M_air-молярнаямассасухоговоздухастандартногосостава.

В () приведенызначениямолярноймассыкомпонентовприродногогаза. В () приведенсоставстандартноговоздуха; рассчитанноезначениеM_airравно
28,9626 кг·кмоль-1.

Плотностьидеальногогазазависитотеготемпературыtидавленияр, иеевычисляютпоформуле

где

ρ° (t, p) -плотностьидеальногогаза;

R-универсальнаягазоваяпостоянная, равная 8,314510 Дж·моль-1·К-1, ();

T = (t+ 273,15) -абсолютнаятемпература, К.

ЧислоВоббеидеальногогазавычисляютпоформуле

где

W°-числоВоббеидеальногогаза;

-вычисляютпоформулам, приведеннымв

Как читать обобщенную диаграмму сжимаемости [ править ]

Чтобы прочитать диаграмму сжимаемости, необходимо знать пониженное давление и температуру. Если пониженное давление или температура неизвестны, необходимо найти уменьшенный удельный объем. В отличие от пониженного давления и температуры, уменьшенный удельный объем не определяется с помощью критического объема. Приведенный удельный объем определяется как

νR=νactualRTcrPcr{\displaystyle \nu _{R}={\frac {\nu _{\text{actual}}}{RT_{\text{cr}}/P_{\text{cr}}}}}

где — удельный объем. νactual{\displaystyle \nu _{\text{actual}}}

После нахождения двух из трех уменьшенных свойств можно использовать диаграмму сжимаемости. На диаграмме сжимаемости пониженное давление находится по оси x, а Z — по оси y. При заданных пониженных давлении и температуре найдите данное давление по оси абсцисс. Оттуда двигайтесь вверх по диаграмме, пока не найдете заданную пониженную температуру. Z можно найти, посмотрев, где эти две точки пересекаются. тот же процесс можно выполнить, если уменьшить удельный объем при пониженном давлении или температуре.

Коэффициент сжимаемости воздуха

Коэффициент сжимаемости воздуха (экспериментальные значения)

	Абсолютное давление (бар)
Температура (K)	1	5	10	20	40	60	80	100	150	200	250	300	400	500
75	0,0052	0,0260	0,0519	0,1036	0,2063	0,3082	0,4094	0,5099	0,7581	1.0125
80		0,0250	0,0499	0,0995	0,1981	0,2958	0,3927	0,4887	0,7258	0,9588	1,1931	1,4139
90	0,9764	0,0236	0,0453	0,0940	0,1866	0,2781	0,3686	0,4681	0,6779	0,8929	1,1098	1,3110	1,7161	2,1105
100	0,9797	0,8872	0,0453	0,0900	0,1782	0,2635	0,3498	0,4337	0,6386	0,8377	1,0395	1,2227	1,5937	1,9536
120	0,9880	0,9373	0,8860	0,6730	0,1778	0,2557	0,3371	0,4132	0,5964	0,7720	0,9530	1,1076	1,5091	1,7366
140	0,9927	0,9614	0,9205	0,8297	0,5856	0,3313	0,3737	0,4340	0,5909	0,7699	0,9114	1,0393	1,3202	1,5903
160	0,9951	0,9748	0,9489	0,8954	0,7803	0,6603	0,5696	0,5489	0,6340	0,7564	0,8840	1.0105	1,2585	1,4970
180	0,9967	0,9832	0,9660	0,9314	0,8625	0,7977	0,7432	0,7084	0,7180	0,7986	0,9000	1,0068	1,2232	1,4361
200	0,9978	0,9886	0,9767	0,9539	0,9100	0,8701	0,8374	0,8142	0,8061	0,8549	0,9311	1.0185	1,2054	1,3944
250	0,9992	0,9957	0,9911	0,9822	0,9671	0,9549	0,9463	0,9411	0,9450	0,9713	1,0152	1.0702	1,1990	1,3392
300	0,9999	0,9987	0,9974	0,9950	0,9917	0,9901	0,9903	0,9930	1,0074	1,0326	1,0669	1,1089	1,2073	1,3163
350	1,0000	1.0002	1 0004	1,0014	1,0038	1,0075	1.0121	1.0183	1,0377	1,0635	1.0947	1,1303	1,2116	1,3015
400	1.0002	1,0012	1,0025	1,0046	1.0100	1,0159	1.0229	1.0312	1,0533	1,0795	1,1087	1,1411	1,2117	1,2890
450	1.0003	1,0016	1,0034	1,0063	1,0133	1.0210	1,0287	1,0374	1,0614	1.0913	1,1183	1,1463	1,2090	1,2778
500	1.0003	1,0020	1,0034	1,0074	1,0151	1.0234	1.0323	1,0410	1,0650	1.0913	1,1183	1,1463	1,2051	1,2667
600	1 0004	1,0022	1,0039	1 0081	1,0164	1.0253	1.0340	1,0434	1,0678	1.0920	1,1172	1,1427	1,1947	1,2475
800	1 0004	1,0020	1,0038	1,0077	1,0157	1.0240	1.0321	1.0408	1,0621	1,0844	1,1061	1,1283	1,1720	1,2150
1000	1 0004	1,0018	1,0037	1,0068	1,0142	1.0215	1.0290	1.0365	1,0556	1,0744	1.0948	1,1131	1,1515	1,1889

Щелкните миниатюру, чтобы увеличить ее.

4.2 Вычисление коэффициента сжимаемости

Длязначенияобъемнойтеплотысгораниятребуетсявтораяпоправка, учитывающаяотличиеобъемамоляреальногогазаотобъемамоляидеальногогаза, этойпоправкойпренебрегатьнельзя. Она
требуетсятакжепривычислениизначенийплотности, относительнойплотностиичислаВоббе. В () приведенообоснованиеспособавведенияпоправокнаобъем, обусловленных
неидеальностьюгаза, рассматриваютсяпринципыихвведенияиприменяемыеупрощения, которые
даютвозможностьвыполнитьвычислениябезприменениякомпьютерныхпрограмм.

Такиепоправкинаобъем, обусловленныенеидеальностьюгаза, вводятспомощьюкоэффициента
сжимаемостиZ_mix. КоэффициентсжимаемостиZ_mixдлястандартныхусловийизмерений, рассматриваемыхв-, рассчитываютпоследующейформуле (илипоформуле () )

гдесуммированиепроводятповсемNкомпонентамсмеси. Значениятакназываемогокоэффициента
суммированияприведеныв () длятрехстандартныхусловийизмерений, представляющихобщийинтерес, длявсехкомпонентовприродногогазаиимитатораприродногогаза, рассматриваемыхвнастоящемстандарте. Приведенытакжезначениякоэффициентовсжимаемостивсех
чистыхкомпонентов (илигипотетическогокоэффициентасжимаемости) Z_j, наосновекоторыхбылиполученызначенияb_j, исходяизсоотношенияb_j = 1 — Z_j, Болееподробнорекомендациипорасчетукоэффициентасжимаемостиприведеныв ().

5 Вычисление молярной
теплоты сгорания

Методы определения вязкости жидкости

Совокупность методов измерения вязкости называют вискозиметрией, и приборы, используемые для таких целей — вискозиметрами.

1. Капиллярные методы основаны на законе Пуазейля и заключаются в измерении времени протекания через капилляр жидкости известной массы под действием силы тяжести при определенном перепаде давлений.

Вискозиметр Оствальда.

Вискозиметр Оствальда представлен на рисунке 7.

С помощью вискозиметра Оствальда определяют вязкость исследуемой жидкости относительным методом. Измеряют время истечения определенного объема (между двумя метками 2, см. рис. 7.) исследуемой и эталонной жидкостей t и t0 соответственно. Объемы жидкостей равны:

где р=gl и р0=0gl перепад давлений для исследуемой и эталонной жидкостей.

Выразим из формулы величину вязкости исследуемой жидкости:

(22)

где 0- вязкость эталонной жидкости, в качестве которой чаще всего используют дистиллированную воду.

Вискозиметр ВК-4.

Вискозиметр Оствальда требует много исследуемой жидкости. В клинической практике используют вискозиметр (рис. 8). Капиллярный вискозиметр ВК-4 применяется для определения вязкости крови.

Рис. 8. Внешний вид вискозиметра ВК-4.

1 и 2 — градуированные пипетки, 3 — подставка, 4 — кран, 5 — резиновая трубка, через которую отсасывают воздух из прибора.

Принцип действия вискозиметра ВК-4 состоит в том, что путь, пройденный жидкостью в капиллярах одинакового сечения при одинаковых давлениях и температурах, обратно пропорционален внутреннему трению или вязкости. Отсюда:

(23)

Измерив пути l0 и l, пройденные дистиллированной водой и кровью, и зная вязкость 0 дистиллированной воды, находят вязкость крови.

1) Метод падающего шарика (метод Стокса)

Метод основан на измерении скорости падения маленьких шариков в исследуемой жидкости (рис. 9).

На падающий шарик радиусом r из вещества с плотностью в вязкой жидкости с плотностью 0 и вязкостью действуют силы:

— сила тяжести ,

— выталкивающая сила ,

— сила сопротивления жидкости, которая, согласно закону Стокса, равна FB=6 rV, где V- скорость шарика.

Рис. 9. Схема для объяснения принципа метода Стокса

При равномерном движении шарика Fтяж = FA + FB , откуда

. (24)

Метод применяется при изучении оседания взвешенных частиц (крахмальных зерен, порошка какао и т. п.).

2) Ротационные методы

Измерение вязкости ротационным вискозиметром основано на определении скорости вращения цилиндра, опущенного в вязкую жидкость.

Сжимаемость

Сжимаемость — это способность жидкости изменять свой объем под действием давления. Сжимаемость капельных жидкостей и газов существенно различается. Так, капельные жидкости при изменении давления изменяют свой объем крайне незначительно. Газы, наоборот, могут значительно сжиматься под действием давления и неограниченно расширяться при его отсутствии.

Для учета сжимаемости газов при различных условиях могут быть использованы уравнения состояния газа или зависимости для политропных процессов.

Сжимаемость капельных жидкостей характеризуется коэффициентом объемного сжатия β_р (Па-1):

где dV — изменение объема под действием давления; dр — изменение давления; V — объем жидкости.

Знак «минус» в формуле обусловлен тем, что при увеличении давления объем жидкости уменьшается, т.е. положительное приращение давления вызывает отрицательное приращение объема.

При конечных приращениях давления и известном начальном объеме V можно определить конечный объем жидкости:

а также ее плотность

Величина, обратная коэффициенту объемного сжатия β_р, называется объемным модулем упругости жидкости (или модулем упругости) К = 1/ β_р (Па).

Эта величина входит в обобщенный закон Гука, связывающий изменение давления с изменением объема

Модуль упругости капельных жидкостей изменяется при изменении температуры и давления. Однако в большинстве случаев K считают постоянной величиной, принимая за нее среднее значение в данном диапазоне температур или давлений.

Модули упругости некоторых жидкостей (МПа):

бензин	1300
керосин	1280
вода	2000
ртуть	32400
масло гидросистем (АМГ-10)	1300
масло индустриальное 20	1360
масло индустриальное 50	1470
масло турбинное	1700

Формула жидкости

Страницы:| 01 |

Многочисленные формулы предлагались изобретательными исследователями многие годы, и каждая формула имела свои преимущества и недостатки. Следующие 6 формул (таблица 1) выбраны, чтобы проиллюстрировать эволюцию концепции инфузионной терапии у детей с ожогами. Первые три формулы теперь имеют историческое значение, а остальные три использовались в настоящее время. В приложении дается более полный список формул.

Коуп и Мур (1947) были первыми, кто начали составлять формулу. Они первыми попытались сопоставить какое количество жидкости требуется на площадь ожоговой поверхности и дали убедительные подтверждения тому, сколько жидкостей нужно перелить больному в первые 48 часов. С годами они обнаружили, что их больные бывают перегружены жидкостью, поэтому максимально рекомендовали, расход жидкостей от 10 — 12 % веса тела в литрах жидкости.

Эванс (1952) разработал свою формулу используя данные Коупа и Мура, на основе состава жидкости ожоговых волдырей. Кроме этого он давал дневное количество жидкостей и ограничивал максимум жидкости, даваемой на ожог, который рассчитывался исходя из 50 % ожоговой поверхности.

Реисс (1953) работая в Военном госпитале ожогового отделения в Бруке, используя формулу Эванса в первые 48 часов, наполовину. Впоследствии ожоговое отделение в Бруке (Пруитт, 1970) исключило назначения коллоидных растворов в первые 24 часа, используя только один раствор Рингер лактата.

Бакстер (1968) предложил инфузионную терапию, используя большое количество только Рингер лактата, измеряя диурез и оценивая клиническое состояние, в первые 24 часа. Он добавлял коллоид в течение первых суток. Опыт показал, что эта формула может использоваться во многих случаях. Проблемы появляются когда ребенка перегружают жидкостью, дают слишком много жидкости сильно обожженному больному.

Карвагал (1975) считает, что введение жидкостей должно быть основано исключительно на расчете поверхности тела. Его формула, в которой используется один раствор, требует 2-х рассчетов: один — процент поверхности ожогов — ожоговое содержание; и другой расчет основан на общей площади поверхности тела — физиологическая потребность. Он рекоммендует раннее применение коллоида (альбумина) и считает, что формула имеет особые преимущества для ожоговых больных всех возрастов и с разной степенью ожога

При использовании этой формулы важно аккуратно вести оценку площади поверхности тела

Боусер и Колдуелл (1983) отстаивает применение гипертонического раствора для реанимации, особенно у детей с ожогами. Они считают, что при таком режиме избегается перегрузка жидкостью, и восстанавливаются потерянные ионы натрия. Поддержка нормальной осмолярности сыворотки и отношение нормальной внутриклеточной жидкости к экстра-клеточной считается преимуществом. Использование гипертонической жидкости для реанимации детей требует постоянного мониторинга за больным, чтобы избежать гипернатремии, гипертонических синдромов и возможных синдромов центральной нервной системы. Никаких коллоидов в первые 48 часов не применялось.

Теоретические модели [ править ]

Вириальное уравнение особенно полезно для описания причин неидеальности на молекулярном уровне (очень немногие газы являются одноатомными), поскольку оно выводится непосредственно из статистической механики:

Z=1+BVm+CVm2+DVm3+…{\displaystyle Z=1+{\frac {B}{V_{\mathrm {m} }}}+{\frac {C}{V_{\mathrm {m} }^{2}}}+{\frac {D}{V_{\mathrm {m} }^{3}}}+\dots }

Где коэффициенты в числителе известны как вириальные коэффициенты и являются функциями температуры.

Вириальные коэффициенты учитывают взаимодействия между последовательно увеличивающимися группами молекул. Например, учитывает взаимодействия между парами, взаимодействия между тремя молекулами газа и так далее. Поскольку взаимодействия между большим числом молекул редки, вириальное уравнение обычно усекается после третьего члена. B{\displaystyle B}C{\displaystyle C}

Коэффициент сжимаемости связан с потенциалом межмолекулярной силы φ следующим образом:

Z=1+2πNAVm∫∞(1−exp⁡(φkT))r2dr{\displaystyle Z=1+2\pi {\frac {N_{\text{A}}}{V_{\text{m}}}}\int _{0}^{\infty }\left(1-\exp \left({\frac {\varphi }{kT}}\right)\right)r^{2}dr}

В статье о реальном газе представлены более теоретические методы вычисления коэффициентов сжимаемости.

Определение и физическое значение

Графическое представление поведения газов и того, как это поведение связано с коэффициентом сжимаемости.

Коэффициент сжимаемости часто определяется в термодинамике и технике как:

Zзнак равнопρрспецифическийТ,{\ displaystyle Z = {\ frac {p} {\ rho R _ {\ text {specific}} T}},}

где p — давление, — плотность газа, — , являющаяся молярной массой , а — ( шкала Кельвина или Ренкина ).
ρ{\ displaystyle \ rho}рспецифическийзнак равнорM{\ displaystyle R _ {\ text {specific}} = {\ frac {R} {M}}}M{\ displaystyle M}Т{\ displaystyle T}

В статистической механике описание таково:

Zзнак равнопVпрТ{\ displaystyle Z = {\ frac {pV} {nRT}}}

где p — давление, n — количество молей газа, — абсолютная температура , — газовая постоянная .
Т{\ displaystyle T}р{\ displaystyle R}

Для идеального газа коэффициент сжимаемости определяется по определению. Во многих реальных приложениях требования к точности требуют учета отклонений от поведения идеального газа, т. Е. От поведения реального газа . Значение обычно увеличивается с давлением и уменьшается с температурой. При высоких давлениях молекулы сталкиваются чаще. Это позволяет силам отталкивания между молекулами оказывать заметное влияние, делая молярный объем реального газа ( ) больше, чем молярный объем соответствующего идеального газа ( ), что приводит к превышению единицы. Когда давление ниже, молекулы могут двигаться. В этом случае преобладают силы притяжения, составляющие . Чем ближе газ к критической точке или точке кипения, тем больше отклонений от идеального.
Zзнак равно1{\ displaystyle Z = 1}Z{\ displaystyle Z}Vм{\ Displaystyle V _ {\ mathrm {m}}}(Vм)идеальный газзнак равнорТп{\ displaystyle (V _ {\ mathrm {m}}) _ {\ text {идеальный газ}} = RT / p}Z{\ displaystyle Z}Z<1{\ Displaystyle Z <1}Z{\ displaystyle Z}

Летучесть

Коэффициент сжимаемости связан с летучестью соотношением

жзнак равнопexp⁡(∫Z-1пdп){\ displaystyle f = P \ exp \ left (\ int {\ frac {Z-1} {P}} dP \ right)}

Рекомендуемые файлы

FREE

Сборник задач под ред. И.И. Куколевского, Л.Г. Подвидза. 2002
Куколевский (Гидравлика)
-38%

Гидравлический расчет гидросистемы комплекса средств обеспечения мобильной доставки питьевой воды населению
Механика жидкости и газа (МЖГ или Гидравлика)

ДЗ №1 Сопло Лаваля (каф Э3)
Механика жидкости и газа (МЖГ или Гидравлика)

Гидравлический расчет гидросист. комплекса средств обесп. мобил доставки питьевой воды населению
Механика жидкости и газа (МЖГ или Гидравлика)

Вариант 48 ТЕМА: Гидравлический расчет гидросистемы комплекса средств обеспечения мобильной доставки питьевой воды населению
Механика жидкости и газа (МЖГ или Гидравлика)

Определить число Рейнольдса и режим движения для потока жидкости, проходящего в трубе с расходом Q=28 л/с. Внутренний диаметр трубы d=200 мм, кинематический коэффициент вязкости жидкости ν=0,012 см2/с. Критическое значение числа Рейнольдса 2000.
Гидравлика

Характерной особенностью изучения сжимаемых жидкостей является необходимость учитывать соотношение между давлением p, плотностью (объемным   весом)  g  = gr, удельным   объемом    и температурой T °К (Кельвина). Это соотношение называется уравнением состояния.

Для идеального газа уравнение состояния (уравнение Менделеева –Клайперона) :

        или       

 где:  R = 29,27 м/°К — газовая постоянная;

          g = 9,81 м/c2 — ускорение силы тяжести.

Далее мы будем рассматривать быстропротекающие процессы, которые с большой точностью можно считать протекающими без обмена теплом, как с внешней средой так и между частями газа (жидкости) внутри, т.е. адиабатическими или изоэнтропическими (эти понятия совпадают для идеального газа), когда dS= 0.

Для газа уравнение состояния при изоэнтропических процессах

где  — отношение теплоемкостей при постоянном давлении (c_p) и                         при постоянном объеме (c_v).

Для воды уравнение изоэнтропы, вытекающее из приведённого выше уравнения состояния, имеет вид:

      или      

С учетом приведенных уравнений изоэнтропы имеем:

 — для воздуха 

 — для воды  

Т.о. скорость звука равна:

— в воздухе

— в воде                                    

При    стандартных    условиях:    p = 1,0332.104 кгс/м2,  плотность   воздуха

r =gg= 1,23 кгс/м3/9,81 м/с2 = 0,125 кгс.с2/м4, k = 1,4 ,

Плотность воды r = 1000/9,81 = 102 кгс.с2/м4, n* = 7,15, B = 3045 кгс/см2,

3.1.2. Число Маха

Многие свойства потока сжимаемой жидкости и характер взаимодействия его с окружающей средой зависят от соотношения скорости движения потока и скорости звука в нем.

Учитывая важность этого обстоятельства, в гидродинамике сжимаемой жидкости рассматриваются два вида одномерного движения потоков:

— дозвуковое течение, когда скорость движения потока меньше скорости звука;   и

— сверхзвуковое течение, когда скорость движения потока превосходит скорость звука в нем.

Сжимаемость жидкости часто характеризуют безразмерной величиной, равной отношению скорости потока сжимаемой жидкости w к скорости звука в нем a. Это отношение называют числом Маха или числом М:

Если  M < 1 — поток считается дозвуковым,

          М > 1- сверхзвуковым.

3.1.4. Уравнение Д.Бернулли для газов

При установившемся одномерном плавноизменяющемся адиабатичесеком движении газа, как и для несжимаемой жидкости, можно поток разбить на элементарные струйки. При этом живые сечения потока можно считать плоскими. Для такого потока газа будут справедливы уравнения Д.Бернулли:

в интегральной форме вдоль потока

Рекомендация для Вас — 6. Метод гибридизации.

в дифференциальной форме

уравнение неразрывности (постоянства массы)

Показатели сжимаемости грунта

Характеристики почвы на деформацию определяются двумя методами:

1. В жестких, не поддающихся растяжению, компрессионных устройствах. В них полностью исключается боковое расширение.
2. В условиях возможного бокового расширения.

Степень сжатия периодически увеличивают, после каждой нагрузке дают время на стихание процесса деформации. После стабилизации измеряют осадку и выводят компрессионную кривую.

К показателям деформирования породы относят:

• коэффициент сжимаемости;
• относительной сжимаемости;
• модуль деформации;
• структурную прочность.

Коэффициент сжимаемости

Первый показатель, изменение рыхлости породы под давлением, крайне важен. Он определяет зависимость конечного деформирования почвенной смеси от давления и дает возможность установить формат осадка основания строения.

Коэффициент относительной сжимаемости

Это параметр деформации относительно единицы давления. При определении этого показателя учитывают: усадку образца под разным нажимом от 0 до p1, начальную высоту исследуемого материала в мм и уровень пористости.

Коэффициент сжимаемости, m0, связан с модулем поперечной деформации E0 (упругости). Степень поперечного расширения для разных песков, супесей, суглинков, глин, отличается.

Выделяют три категории грунта:

1. сильно сжимаемый – m > 0,5 (МПа)-1
2. средне сжимаемый – 0,1>m > 0,5 (МПа)-1
3. мало сжимаемый – m < 0,5 (МПа)-1

Модуль упругости

Эта величина переменная. Она меняется: от степени сдавливания, времени воздействия, плотности породы, площади штампа. Чтобы спрогнозировать поведение почвенного слоя в условиях сдавливания, необходимо знать эти показатели.

Структурная прочность

Степень уплотнения зависит от структуры почвы, рыхлости, наличия кристаллизационных связей. Структурная прочность – это параметр напряженности, при котором происходит разрушение связей. Небольшие нагрузки вызывают легкую деформацию, при этом коэффициент пористости практически остается неизменным. При усилении нагрузок и достижении структурной прочности происходит перекомпоновка частиц, уплотнение и уменьшение пористости.

6.1 Идеальный газ

Значениемассовойтеплотысгоранияидеальногогаза, определяемоеисходяиззначениймассовойдоликомпонентовсмесиизвестногосостава, притемпературеt₁вычисляютпоформуле

где

-значениеидеальной (высшейилинизшей) теплотысгораниясмеси, рассчитанноеисходя
иззначениймассовойдоликомпонентовгаза;

М -молярнаямассасмеси, которуювычисляютпоформуле

где

x_j-молярнаядоля j-гокомпонента;

M_j-молярнаямассаj-гокомпонента.

В () приведенызначениямолярноймассыдлявсехкомпонентов, рассматриваемыхвнастоящемстандарте.

Применениеформул (5) и (6) являетсяосновнымспособомвычисления. Приальтернативном
методеиспользуютформулу

где

являетсязначениемидеальной (высшейилинизшей) теплотысгорания, рассчитаннымна
основезначениямассовойдолиj-гокомпонента.

Дляудобствазначениямдлячетырехзначенийt₁ (25°С, 20°С, 15°Си°С) приведеныв (), чтобыпользовательмогизбежатьнеобходимостиприменятьзначениявкачестве исходнойточкивычисления.

Числовыезначения, полученныеполюбомуизэтихметодов, будутиметьрасхождениенеболее
0,01 МДж·кг -1, котороесоответствуетточностисовременногоуровнятехники.