Что такое погрешность в физике?

Введение

Все, что сказано в этом введении, запоминать не нужно. это справочный материал, к которому вы будете обращаться при выполнении лабораторных работ.

1. Как определять погрешности измерений

Выполнение лабораторных работ связано с измерением различных физических величин и последующей обработкой их результатов.

Измерение — нахождение значения физической величины опытным путем с помощью средств измерений.

Прямое измерение — определение значения физической величины непосредственно средствами измерения.

Косвенное измерение — определение значения физической величины по формуле, связывающей ее с другими физическими величинами, определяемыми прямыми измерениями.

Введем следующие обозначения:

A, B, C, … — физические величины.

A_пр — приближенное значение физической величины, т.е. значение, полученное путем прямых или косвенных измерений.

ΔA — абсолютная погрешность измерения физической величины.

ε — относительная погрешность измерения физической величины, равная:

Δ_иA — абсолютная инструментальная погрешность, определяемая конструкцией прибора (погрешность средств измерения; указывается в каждой работе при описании прибора в разделе Оборудование и средства измерения)

Δ_оA — абсолютная погрешность отсчета (получающаяся от недостаточно точного отсчета показаний средств измерения), она равна в большинстве случаев половине цены деления; при измерении времени — цене деления секундомера или часов.

Максимальная абсолютная погрешность прямых измерений складывается из абсолютной инструментальной погрешности и абсолютной погрешности отсчета при отсутствии других погрешностей:

ΔA=Δ_иA + Δ_оA

Абсолютную погрешность измерения обычно округляют до одной значащей цифры (ΔA≈0,17=0,2); численное значение результата измерений округляют так, чтобы его последняя цифра оказалась в том же разряде, что и цифра погрешности (А=10,332≈10,3).

Результаты повторных измерений физической величины А, проведенных при одних и тех же контролируемых условиях и при использовании достаточно чувствительных и точных (с малыми погрешностями) средств измерения, отличаются друг от друга.

В этом случае A_пр находят как среднее арифметическое значение всех измерений, а ΔA (ее в этом случае называют случайной погрешностью) определяют методами математической статистики.

В школьной лабораторной практике такие средства измерения практически не используются. Поэтому при выполнении лабораторных работ необходимо определять максимальные погрешности измерения физических величин. При этом для получения результата достаточно одного измерения.

Относительная погрешность косвенных измерений определяется, как показано в таблице 1.

Абсолютная погрешность косвенных измерений определяется по формуле ΔA=A_прε (ε выражается десятичной дробью).

Таблица 1

Формулы для нахождения относительной погрешности косвенных измерений

Nº п/п	Формула физической величины	Формула относительной погрешности
1
2
3	A=B+C
4

2. О классе точности электроизмерительных приборов

Для определения абсолютной инструментальной погрешности прибора надо знать его класс точности. Класс точности γ_пр измерительного прибора показывает, сколько процентов составляет абсолютная инструментальная погрешность Δ_иA от всей шкалы прибора (A_max):

Класс точности указывается при описании прибора в разделе Оборудование и средства измерения. Cуществуют следующие классы точности электроизмерительных приборов: 0,1; 0,2; 0,5; 1; 1,5; 2,5; 4. Зная класс точности прибора (γ_пр) и всю его шкалу (A_max), определяют абсолютную погрешность Δ_иA измерения физической величины А этим прибором:

3. Как сравнивать результаты измерений

1. Записать результаты измерений в виде двойных неравенств:

A_{1 пр} – ΔA₁ < A_{1 пр} < A_{1 пр} + ΔA₁
A_{2 пр} – ΔA₂ < A_{2 пр} < A_{2 пр} + ΔA₂
2. Сравнить полученные интервалы значений (рис.1): если интервалы не перекрываются, то результаты неодинаковы, если перекрываются — одинаковы при данной относительной погрешности измерений.

Рисунок 1.

4. Как оформлять отчет о проделанной работе

Отчетом о проделанной работе является форма, находящаяся в левом нижнем окне. После ее заполнения надо нажать на кнопку «Отправить результаты на сервер».

Значения измеренных физических величин переносятся в таблицу результатов автоматически после нажатия соответствующей кнопки.

Значения остальных величин и ответ на контрольный вопрос вводятся с клавиатуры.

домашней странице BARSIC

Абсолютная и относительная погрешность

Абсолютной погрешностью или, короче, погрешностью приближенного
числа называется разность между этим числом и его точным значением (из большего числа вычитается меньшее)*.

Пример 1. На предприятии 1284 рабочих и служащих. При
округлении этого числа до 1300 абсолютная погрешность
составляет 1300 — 1284 = 16. При округлении до 1280 абсолютная погрешность составляет 1284 — 1280 = 4.

Относительной погрешностью приближенного числа называется отношение
абсолютной погрешности приближенного числа к самому этому числу.

Пример 2. В школе 197 учащихся. Округляем это число до 200. Абсолютная
погрешность составляет 200 — 197 = 3. Относительная погрешность равна 3/197 или, округленно, 3/197 = 1,5 %.

В большинстве случаев невозможно узнать точное значение приближенного числа, а значит, и точную величину погрешности.
Однако почти всегда можно установить, что погрешность (абсолютная или относительная) не превосходит некоторого числа.

Пример 3. Продавец взвешивает арбуз на чашечных весах. В наборе гирь наименьшая — 50 г. Взвешивание дало 3600 г. Это число – приближенное. Точный вес арбуза
неизвестен. Но абсолютная погрешность не
превышает 50 г. Относительная погрешность не превосходит 50/3600 ≈ 1,4%.

Число, заведомо превышающее абсолютную погрешность (или в худшем случае равное ей), называется предельной абсолютной погрешностью. Число, заведомо превышающее
относительную погрешность (или в худшем случае равное ей), называется предельной относительной погрешностью.

В примере 3 за предельную абсолютную погрешность можно взять 50 г, а за предельную относительную погрешность — 1,4 %.

Величина предельной погрешности не является вполне определенной. Так, в примере 3 можно принять за предельную абсолютную
погрешность 100 г, 150 г и вообще всякое число, большее чем 50 г. На практике берется по возможности меньшее значение
предельной погрешности. В тех случаях, когда известна точная величина погрешности, эта величина служит одновременно
предельной погрешностью. Для каждого приближенного числа должна быть известна его предельная погрешность
(абсолютная или oотносительная). Когда она прямо не указана, подразумевается что предельная абсолютная погрешность
составляет половину единицы последнего выписанного разряда. Так, если приведено приближенное число 4,78 без указания
предельной погрешности, то подразумевается, что предельная абсолютная погрешность составляет 0,005. Вследствие этого
соглашения всегда можно обойтись без указания предельной погрешности числа.

Предельная абсолютная погрешность обозначается греческой буквой Δ («дельта»); предельная относительная
погрешность — греческой буквой δ («дельта малая»). Если приближенное число обозначить буквой а, то

δ = Δ/a.

Пример 4. Длина карандаша измерена линейкой с миллиметровыми делениями. Измерение показало 17,9 см. Какова предельная
относительная погрешность этого измерения?
Здесь а = 17,9 см; можно принять Δ = 0,1 см, так как с точностью до 1 мм измерить карандаш нетрудно, a значительно уменьшить, предельную погрешность ни удастся (при навыке можно прочесть на хорошей линейке и 0,02 и даже 0,01 см, но у самого карандаша ребра могут разниться на бoльшую величину). Относительная погрешность равна 0,1/17,9.
Округляя, находим δ = 0,1/18 ≈ 0,6%.

Пример 5. Цилиндрический поршень имеет около 35 мм в диаметре. С какой точностью нужно его измерить микрометром, чтобы
предельная относительная погрешность составляла 0,05%?Решение. По условию, предельная абсолютная погрешность должна составлять 0,05% от 35 мм. Следовательно, предельная
абсолютная погрешность равна 36*(0,05/100) = 0,0175 (мм) или, усиливая, 0,02 (мм). Можно воспользоваться
формулой δ = Δ/a.
Подставляя в неё а = 35, δ = 0,0005, имеем 0,0005 = Δ/35. Значит, Δ = 35 • 0,0005 = 0,0175 (мм).

* Иначе говоря, если a есть приближенное число, а х – его точное значение, то абсолютная погрешность есть абсолютное
значение разности a – х. В некоторых руководствах абсолютной погрешностью называется сама
разность a – х (или разность х — a). Эта величина может быть положительной или отрицательной.

Формула погрешности

Таким образом, общая формула для записи величин с погрешностью выглядит следующим образом:

$$X = x \pm \Delta x$$

где $X$ — измеряемая величина, $x$ — результат измерений, $\Delta x$ — погрешность. 

Выходит, что истинное значение длины карандаша располагается в диапазоне значений от 11.5 см до 12.5 см.

При более точных замерах до миллиметра: от 12.15 см до 12.25 см.

Однако остается один последний интересный момент. Несмотря на то, что мы провели замеры и определили длину, философски говоря, вопрос остается вопросом: так какую же точную длину имеет карандаш?

Таковы погрешности. Где-то от, где-то до. 

А точно — никак.

Влияние косвенных факторов

Существуют факторы, которые косвенно влияют на результат измерения и не входят в состав измеряемой величины.
Например, при измерении длины профиля, длина профиля зависит от температуры профиля, а результат измерения
в косвенной форме зависит от температуры микрометра. В таком случае, в результате замера должна быть описана температура,
при которой производился замер. Другой пример: при измерении длины профиля с помощью лазера на результат измерения
косвенно влияют температура воздуха, атмосферное давление и влажность воздуха.

Таким образом, что бы результат измерения был репрезентативен, необходимо определить условия измерения:
определить факторы, влияющие на измерение; выбрать соответствующие инструменты; определить измеряемый
объект; использовать соответствующий режим работы. Такие условия измерений определяются нормами для
того, что бы результаты измерений можно было воспроизвести и сравнить, такие условия называются
нормальными условиями для измерения.

Источники погрешностей

Рассмотрим различные причины возникновения погрешностей.

Математическая модель задачи является неточной

Погрешность возникает из-за того, что сам численный метод или математическая модель является лишь приближением к точному методу (например, дифференцирование). Кроме того, любая математическая модель или метод могут внести существенные погрешности, если в ней не учтены какие-то особенности рассматриваемой задачи. Модель может прекрасно работать в одних условиях и быть совершенно неприемлемой в других. Такую погрешность называют также методической. Она всегда имеет место, даже при абсолютно точных данных и абсолютно точных вычислениях. В большинстве случаев погрешность численного метода можно уменьшить до требуемого значения за счет изменения параметров метода (например, уменьшением шага дискретизации, или увеличением количества итераций).

Ошибки в исходных данных

Исходные данные задачи часто являются основным источником погрешностей. Ошибки такого типа неизбежны и проявляются в любых реальных задачах, поскольку любое измерение может быть проведено с только какой-то предельной точностью. Вместе с погрешностями, вносимыми математической моделью, их называют неустранимыми погрешностями, поскольку они не могут быть уменьшены ни до начала решения задачи, ни в процессе ее решения.

Следует стремиться к тому, чтобы все исходные данные были примерно одинаковой точности. Сильное уточнение одних исходных данных при наличии больших погрешностей в других не приводит к повышению точности конечных результатов. Если какие-то отдельные точки данных (измерения) явно ошибочные, их можно исключить из вычислений.

Вычислительные ошибки (ошибки округления)

Ошибки этого типа проявляются из-за дискретной (а не непрерывной) формы представления величин в компьютере. Вычислительные ошибки можно свести к минимуму продуманно организовывая алгоритмы.

Понятие и классификация

Под термином погрешность принято понимать степень отклонения реальной величины от вычисленной. Этот показатель служит мерой точности измерения.

Существует несколько разновидностей погрешности:

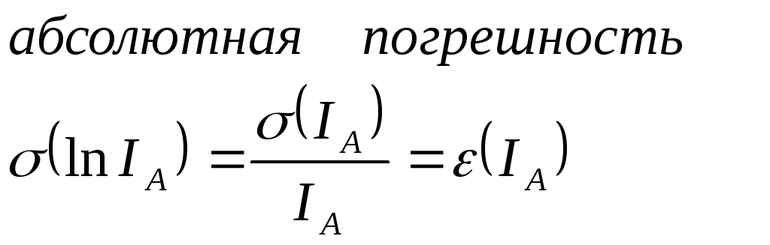
1. Абсолютная — оценка ошибки в абсолютных единицах. Величина ее может быть разной в зависимости от способа расчета.
2. Относительная — отношение абсолютной величины к тому значению, которое принято считать истинным. Измеряется в процентах.
3. Приведенная — разновидность относительной. Ее вычисляют отношением абсолютной и условной постоянной величины, определяется в процентах.
4. Приборная или инструментальная — погрешность, которую дают технические средства измерений. Она обусловлена неточной цифровой градуировкой приборов или недостаточной наглядностью. Класс точности приборов будет равен максимальной приведенной погрешности и выражается в процентах. К примеру, класс точности вольтметра ΔU = ±0,75 В.
5. Методическая — связанная с несовершенством метода измерения или его чрезмерным упрощением.
6. Субъективная или операторная — погрешность, связанная с личными свойствами оператора — невнимательностью, утомлением, профессиональной подготовленностью.
7. Случайная. Погрешность, которая может изменяться при разных измерениях. Изменения возможны по знаку или величине отклонения. Причиной может быть техническое несовершенство приборов отсчета или объекта измерения, неблагоприятные для работы условия или особенности измеряемых единиц.
8. Систематическая. Погрешность, изменения которой имеют некоторую закономерность во времени. В качестве частного случая допускают постоянное отклонение, которое не изменяется во времени.
9. Прогрессирующая или дрейфовая — медленно изменяется во времени и не может быть предсказана. Такое отклонение относится к случайным.
10. Грубая или промах. Значительное отклонение от принятой нормы. Возникает в результате неисправности аппаратуры или ошибки экспериментатора.

Корректирование результатов измерений

В некоторых случаях существует возможность корректирования результата измерения, когда невозможно
соблюдение нормальных условий. Введение такой корректировки усложняет измерение и часто требует
измерения других величин. Например, измерение длины профиля при температуре θ, отличной от нормальной,
20°C, может быть скорректировано следующей формулой: l’₂₀ = l’_θ.
Корректировка калибровки измерительного устройства при 20°C — C_c. Таким образом,
длина профиля определяется такой зависимостью: l₂₀ = f(l’_θ,α,θ,C_c).

В общем виде, результат измерения будет выражен зависимостью от других измерений: y = f(x₁,x₂,…x_N),
где f может быть аналитической функцией, распределением вероятности или даже быть частично неизвестной функцией.
Корректирование результатотв уменьшает неточность измерений, но таким способом невозможно уменьшить неточность измерений до нуля.

Неопределённость измерительного инструмента

Неопределённость может быть определена посредством сравнения результатов замеров с образцом
или замером инструментом более высокой точности. В процессе калибровки инструмента выводится
корректировочное значение и неопределённость.

Пример калибровки микрометра

Замерив образец заранее известной длины, мы получим значение корректировки, c. Таким образом, если длина, измеренная
инструментом равна x, фактическая длина будет равна x_c = x + c.

Произведём n_c замеров образца и получим отклонение s_c. Теперь, при любых замерах
откалиброванным микрометром, значение неопределённости u будет равно:
u = √(u2 + s2_c/n_c + u2_m/n),
u_m — отклонение полученное при n замерах.

Классификация ошибок измерений

_______Измерения в геодезии рассматриваются с двух точек зрения: количественной, выражающей числовое значение измеренной величины, и качественной, характеризующей
ее точность. Из практики известно, что даже при самой тщательной и аккуратной работе многократные (повторные) измерения не дают одинаковых результатов. Это указывает на
то, что получаемые результаты не являются точным значением измеряемой величины, а несколько отклоняются от него. Значение отклонения характеризует точность измерений.

_______При геодезических измерениях неизбежны ошибки. Эти ошибки бывают грубые,
систематические и случайные.

_______ К грубым ошибкам относятся просчеты в измерениях по причине невнимательности
наблюдателя или неисправности прибора, и они полностью должны быть исключены. Это
достигается путем повторного измерения.

_______Систематические ошибки происходят от известного источника, имеют
определенный знак и величину и их можно учесть при измерениях и вычислениях.

_______Случайные ошибки обусловлены разными причинами и полностью исключить их из
измерений нельзя. Поэтому возникают две задачи: как из результатов измерений получить
наиболее точную величину и как оценить точность полученных результатов измерений.
Эти задачи решаются с помощью теории ошибок измерений
_______

_______В основу теории ошибок положены следующие свойства случайных ошибок:_______1. Малые ошибки встречаются чаще, а большие реже._______2. Ошибки не превышают известного предела._______3. Положительные и отрицательные ошибки, одинаковые по абсолютной величине,
одинаково часто встречаются._______4. Сумма ошибок, деленная на число измерений, стремится к нулю при большом числе
измерений.

_______По источнику происхождения различают ошибки приборов, внешние и личные.
Ошибки приборов обусловлены их несовершенством, например погрешность угла,
измеренного теодолитом, неточным приведением в вертикальное положение оси его
вращения.

_______Внешние ошибки происходят из-за влияния внешней среды, в которой протекают
измерения, например погрешность в отсчете по нивелирной рейке из-за изменения
температуры воздуха на пути светового луча (рефракция) или нагрева нивелира
солнечными лучами.

_______Личные ошибки связаны с особенностями наблюдателя, например, разные наблюдатели
по-разному наводят зрительную трубу на визирную цель. Так как грубые погрешности
должны быть исключены из результатов измерений, а систематические исключены
или ослаблены до минимально допустимого предела, то проектирование измерений с
необходимой точностью и оценку результатов выполненных измерений производят,
основываясь на свойствах случайных погрешностей.

Допуск

На производстве используют понятие допуск, устанавливая верхнее и нижнее значение, в пределах которых
измеряемый объект не считается браком. Например, при производстве конденсаторов ёмкостью 100±5% мкФ
устанавливается допуск 5%, это означает, что на этапе контроля качества при замере ёмкости конденсатора,
конденсаторы ёмкостью более 105 мкФ и менее 95 мкФ считаются браком.

При контроле качества необходимо учитывать неопределённость измерительного инструмента, так, если
неопределённость измерения ёмкости конденсатора составляет 2 мкФ, то результат измерения 95 мкФ может
означать 93-97 мкФ. Для учёта неопределённости в результатах измерений необходимо расширить
понятие допуска: в допуске должна быть учтена неопределённость измерительного прибора. Для этого необходимо
задать доверительный интервал, т.е. процент деталей, который должен гарантированно соответствовать заданным
параметрам.

Доверительный интервал строится по нормальному распределению: считается, что результат измерения
соответствует нормальному распределению
μ±kσ. Вероятность нахождения значения в пределах ku зависит от значения k:
при k=1 68,3% измерений попадут в значение σ±u, при k=3 — 99,7%.

Метрологическая лаборатория

Лаборатория метрологии должна контролировать все косвенные факторы измерения. Условия зависят от типа и точности
измерений. Так, лабораторией может считаться даже отдел измерений на производстве. Ниже будет рассказано об
основных требованиях к метрологической лаборатории.

Расположение

Метрологическая лаборатория должна быть расположена максимально удалённо от других зданий, находится
на самом низком этаже (лучше — в подвале) и обладать достаточной изоляцией от шума, перепада температур,
вибраций и других источников раздражения.

Температура

В метрологической лаборатории должен соблюдаться температурный режим, который учитывает находящихся
в лаборатории сотрудников. Необходимо наличие системы кондиционирования воздуха и отопления.

Освещение

Освещение должно производиться люминесцентными лампами холодного цвета, освещённость должна составлять от 800 до 1000 лк.

Методы Корнфельда и Стьюдента

Некоторые экспериментальные исследования требуют многократного измерения одного и того же показателя с помощью аппаратуры или приспособлений. В этом случае высока вероятность возникновения отклонений разброса. Определить ее величины можно разными способами. Самый распространенный и доступный из них называется по автору — методом Корнфельда.

Он применяется в ситуации, когда какая-либо физическая величина была измерена n раз. В этом случае рекомендован следующий порядок действий:

1. Предполагается, что имеется ряд результатов измерений от Х1 до Хn.
2. Из этих величин выбирают минимальную и максимальную.
3. Вычисляют среднее значение Х.
4. В пределах от наименьшего до наибольшего показателя выбирают доверительный интервал.
5. Чтобы найти абсолютное отклонение, необходимо вычесть из максимального результата измерения величину минимального. Полученную разность делят пополам.

Метод Корнфельда имеет существенный недостаток. Чтобы определить вероятность приведенного результата, необходимо провести большое количество измерений. При этом нет возможности изменить границы доверительного интервала. Более точные данные можно получить, используя метод расчета Стьюдента. Для этого используют специальные таблицы, где отражены так называемые коэффициенты Стьюдента.

Что такое точность?

Точность измерений характеризует близость результата измерения к фактическому значению измеряемой величины. Строго говоря, ни одна физическая величина не может быть измерена с абсолютной точностью — так, чтобы данные измерительного прибора отображали истинное значение.

Мир и его явления, на самом деле, практически всегда имеют отношение к иррациональным числам, таким, как, к примеру, результат деления десяти на три: наберите данную операцию на калькуляторе и посмотрите на то, как неэстетично в реальности выглядят данные — с кучей знаков после запятой, за которыми не угнаться.

Однако иррациональность чисел не удивляет, да и слишком абстрактна, дабы уловить суть. Что есть деление десяти на три? Тогда, для конкретности, стоит покуситься на святое — на время. Казалось бы, что может быть точнее времени, показываемого самыми точными на свете часами — атомными часами?

И тем не менее, даже если вы зайдете на онлайн-ресурс, официально регистрирующий международное атомное время с точностью до миллисекунд, действительного точного измерения времени там вы не найдете.

Всегда есть условности: задержка передачи данных между сетевыми элементами; ваш мозг, регистрирующий и обрабатывающий информацию, поступающую через органы чувств и т. д. Все это отдаляет нас, хоть и несущественно, от фактического значения величины.

Именно поэтому в физике одним из важнейших понятий является понятие погрешности.

Математическая погрешность: формула для каждого типа

Если определение погрешности можно провести точным путем, она считается математической. Зачем нужно вычисление этого значения в маркетинге?

Погрешности возникают настолько часто, что популярной практикой в исследованиях является включение значения погрешности в окончательные результаты. Для этого используются формулы. Математическая погрешность — это значение, которое отражает разницу между выборкой и фактическим результатом. Если при расчетах учитывалась  погрешность, в тексте исследования указывается что-то вроде: «Абсолютная погрешность для этих данных составляет 3,25%». Погрешность можно вычислить с любыми цифрами: количество человек, участвующих в опросе, погрешность суммы, затраченной на маркетинговый бюджет, и так далее.

Формулы погрешностей вычисляются следующим образом.

Формула дает разницу между измеренным и реальным значением.

Формула абсолютной погрешности

Относительная погрешность: формула

Формула использует значение абсолютной погрешности и вычисляется в процентах по отношению к фактическому  значению.

Формула относительной погрешности

Приведенная погрешность: формула

Формула также использует значение абсолютной погрешности. В чем измеряется приведенная погрешность? Тоже в процентах, но в качестве «эталона» используется не реальное значение, а единица измерения любой нормирующей шкалы. Например, для обычной линейки это значение равно 1 мм.

Формула приведенной погрешности